
已知函数 ,
,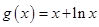 ,其中
,其中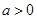 .
.
(1)若 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若对任意的 (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥ 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)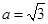 (2)
(2)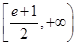
【解析】
试题分析:解:∵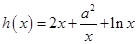 ,其定义域为
,其定义域为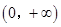 ,
,
∴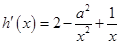 .
.
∵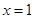 是函数
是函数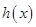 的极值点,∴
的极值点,∴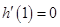 ,
,
即 .
.
∵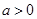 ,∴
,∴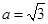 .
.
(2)
对任意的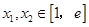 都有
都有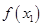 ≥
≥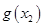 成立等价于对任意的
成立等价于对任意的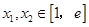
都有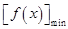 ≥
≥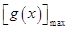 .
.
当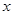
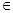 [1,
[1,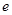 ]时,
]时,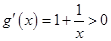 .
.
∴函数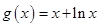 在
在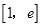 上是增函数.
上是增函数.
∴ .
.
∵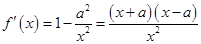 ,且
,且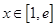 ,
,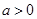 .
.
①当 且
且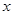
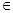 [1,
[1,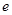 ]时,
]时,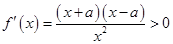 ,
,
∴函数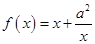 在[1,
在[1,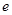 ]上是增函数,
]上是增函数,
∴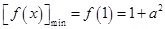 .
.
由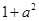 ≥
≥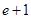 ,得
,得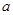 ≥
≥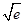 ,
,
又 ,∴
,∴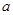 不合题意.
不合题意.
②当1≤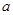 ≤
≤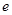 时,
时,
若1≤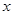 <
<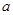 ,则
,则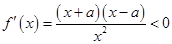 ,
,
若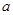 <
<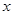 ≤
≤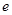 ,则
,则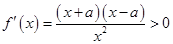 .
.
∴函数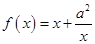 在
在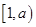 上是减函数,在
上是减函数,在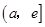 上是增函数.
上是增函数.
∴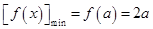 .
.
由 ≥
≥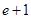 ,得
,得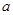 ≥
≥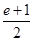 ,
,
又1≤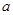 ≤
≤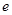 ,∴
,∴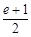 ≤
≤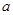 ≤
≤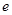 .
.
③当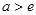 且
且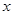
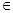 [1,
[1,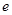 ]时,
]时,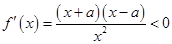 ,
,
∴函数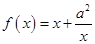 在
在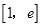 上是减函数.∴
上是减函数.∴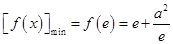 .
.
由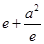 ≥
≥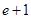 ,得
,得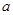 ≥
≥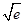 ,
,
又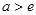 ,∴
,∴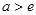 .
.
综上所述,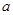 的取值范围为
的取值范围为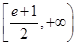 .
.
考点:导数的应用
点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。


科目:高中数学 来源: 题型:
(1)求ω的取值范围;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,a=![]() ,b+c=3(b>c),当ω最大时,f(A)=1,求边b,c的长.
,b+c=3(b>c),当ω最大时,f(A)=1,求边b,c的长.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省五校联盟高三下学期第一次联考文科数学试卷(解析版) 题型:解答题
已知 ,函数
,函数 ,
, ,(其中e是自然对数的底数,为常数),
,(其中e是自然对数的底数,为常数),
(1)当 时,求
时,求 的单调区间与极值;
的单调区间与极值;
(2)是否存在实数 ,使得
,使得 的最小值为3. 若存在,求出
的最小值为3. 若存在,求出 的值,若不存在,说明理由。
的值,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省等三校高三2月月考数学文卷 题型:解答题
(本小题满分14分)
已知函数 ,
, .(其中
.(其中 为自然对数的底数),
为自然对数的底数),
(Ⅰ)设曲线 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值;
(Ⅱ)若对于任意实数 ≥0,
≥0, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)当 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点
处的切线与 轴垂直?若存在,求出
轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年天津市高三十校联考理科数学 题型:解答题
.(14分)已知函数 ,
, ,其中
,其中
(Ⅰ)若 是函数
是函数 的极值点,求实数
的极值点,求实数 的值
的值
(Ⅱ)若对任意的 (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥ 成立,求实数
成立,求实数 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com