
����Ŀ��ij���յĻ�������Ϊa����λ��Ԫ������������ñ��յ�Ͷ���˳�Ϊ�����ˣ������˱���ȵı�����������ȳ��մ����Ĺ������£�
����ȳ��մ��� | 0 | 1 | 2 | 3 | 4 | ��5 |
���� | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
�������һ������һ���ڳ��մ�������Ӧ�������£�
һ���ڳ��մ��� | 0 | 1 | 2 | 3 | 4 | ��5 |
���� | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
��1����һ�����˱���ȵı��Ѹ��ڻ������ѵĸ��ʣ�
��2����һ�����˱���ȵı��Ѹ��ڻ������ѣ����䱣�ѱȻ������Ѹ߳�60%�ĸ��ʣ�
��3���������˱���ȵ�ƽ��������������ѵı�ֵ��
���𰸡�
��1���⣺��ij���յĻ�������Ϊa����λ��Ԫ����
����ȳ��մ������ڵ���2ʱ�������˱���ȵı��Ѹ��ڻ������ѣ�
���ɸ�����һ������һ���ڳ��մ�������Ӧ����ͳ�Ʊ��ã�
һ�����˱���ȵı��Ѹ��ڻ������ѵĸ��ʣ�
p1=1��0.30��0.15=0.55��
��2���⣺���¼�A��ʾ��һ�����˱���ȵı��Ѹ��ڻ������ѡ����¼�B��ʾ��һ�����˱���ȵı��ѱȻ������Ѹ߳�60%����
������P��A��=0.55��P��AB��=0.10+0.05=0.15��
���������һ�����˱���ȵı��Ѹ��ڻ������ѣ�
���䱣�ѱȻ������Ѹ߳�60%�ĸ��ʣ�
p2=P��B|A��= ![]() =
= ![]() =
= ![]() ��
��
��3���⣺�����⣬�����˱���ȵ�ƽ��������������ѵı�ֵΪ��
![]() =1.23��
=1.23��
�������˱���ȵ�ƽ��������������ѵı�ֵΪ1.23
����������1������ȳ��մ������ڵ���2ʱ�������˱���ȵı��Ѹ��ڻ������ѣ��ɴ����ø�����һ������һ���ڳ��մ�������Ӧ����ͳ�Ʊ����ݶ����¼����ʼ��㹫ʽ�����һ�����˱���ȵı��Ѹ��ڻ������ѵĸ��ʣ���2�����¼�A��ʾ��һ�����˱���ȵı��Ѹ��ڻ������ѡ����¼�B��ʾ��һ�����˱���ȵı��ѱȻ������Ѹ߳�60%�������������P��A����P��AB�����ɴ��������������������һ�����˱���ȵı��Ѹ��ڻ������ѣ����䱣�ѱȻ������Ѹ߳�60%�ĸ��ʣ���3�������⣬����������˱���ȵ�ƽ��������������ѵı�ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͬһ�ž��ȵ����ӣ����i�εõ��ĵ���Ϊai �� ������������k��ʹa1+a2+��+ak=6�����kΪ����������֣�
��1���������������Ϊ3�ĸ��ʣ�
��2����k=1������ĵ÷�Ϊ5�֣���k=2������ĵ÷�Ϊ3�֣���k=3������ĵ÷�Ϊ1�֣����������λ�û�ҵ���������������0�֣���÷�X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����һ��
����һ��![]() ��
��![]() ���ϵ���ӰΪ
���ϵ���ӰΪ![]() �е�Ϊ
�е�Ϊ![]() ��
��![]() ��
��
��1����![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() ��
��![]() ��
��![]() ���µ������ν���
���µ������ν���![]() ����
����![]() ����
����![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ���µ������ν���
���µ������ν���![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ��б��֮��Ϊ
��б��֮��Ϊ![]() ����
����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ���Ƿ����
���Ƿ����![]() ʹ��
ʹ��![]() �ɵȱ����У������ڣ���
�ɵȱ����У������ڣ���![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() �ֱ�����Բ
�ֱ�����Բ![]() �����ҽ���.
�����ҽ���.
��1����![]() �Ǹ���Բ�ϵ�һ�����㣬��
�Ǹ���Բ�ϵ�һ�����㣬��![]() �����ֵ����Сֵ��
�����ֵ����Сֵ��
��2���������![]() ��ֱ������Բ���ڲ�ͬ������
��ֱ������Բ���ڲ�ͬ������![]() ��
��![]() ����
����![]() Ϊ��ǣ�����
Ϊ��ǣ�����![]() Ϊ����ԭ�㣩����ֱ��
Ϊ����ԭ�㣩����ֱ��![]() ��б��
��б��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C��DΪƽ���ı���ABCD���ĸ��ڽǣ� 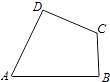
��1��֤����tan ![]() =
= ![]() ��
��
��2����A+C=180�㣬AB=6��BC=3��CD=4��AD=5����tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=x��1��alnx��g��x��= ![]() ��a��0���Ҷ�����x1 �� x2��[3��4]��x1��x2����|f��x1����f��x2��|��|
��a��0���Ҷ�����x1 �� x2��[3��4]��x1��x2����|f��x1����f��x2��|��| ![]() ��
�� ![]() |�ĺ��������ʵ��a��ȡֵ��ΧΪ ��
|�ĺ��������ʵ��a��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C1��x2=y��ԲC2��x2+��y��4��2=1��Բ��Ϊ��M
��1�����M��������C1���ߵľ��룻
��2����֪��P��������C1��һ�㣨����ԭ�㣩������P��ԲC2���������ߣ���������C1��A��B���㣬����M��P�����ֱ��l��ֱ��AB����ֱ��l�ķ��̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������[��3��3]�ϵĵ�������f��x�����㣺�������x��[��3��3]������f��f��x����2x��=6������[��3��3]�����ȡһ��ʵ��x��ʹ��f��x����ֵ��С��4�ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com