
【题目】已知公比为正数的等比数列![]() ,首项
,首项![]() ,前n项和为
,前n项和为![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]()
【答案】(Ⅰ)an=6×(![]() )n,(Ⅱ)Tn=2﹣(n+2)(
)n,(Ⅱ)Tn=2﹣(n+2)(![]() )n
)n
【解析】
(Ⅰ)设公比为q>0,由等比数列的通项公式和等差数列中项的性质,解方程可得q,即可得到所求通项公式;(Ⅱ)求得bn![]() n(
n(![]() )n,运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
)n,运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
(Ⅰ)an=6×(![]() )n,(Ⅱ)Tn=2﹣(n+2)(
)n,(Ⅱ)Tn=2﹣(n+2)(![]() )n
)n
依题意公比为正数的等比数列{an}(n∈N*),首项![]() =3,
=3,
设an=3qn﹣1,
∵![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
∴2(![]() )=
)=![]() +
+![]()
即2(![]() )=(
)=(![]() +(
+(![]() ),
),
化简得4![]() =
=![]() ,
,
从而4q2=1,解得q=±![]() ,
,
∵{an}(n∈N*)公比为正数,
∴q![]() ,an=6×(
,an=6×(![]() )n,n∈N*;
)n,n∈N*;
(Ⅱ)bn![]() n(
n(![]() )n,
)n,
则Tn=1(![]() )+2(
)+2(![]() )2+3(
)2+3(![]() )3+…+(n﹣1)(
)3+…+(n﹣1)(![]() )n﹣1+n(
)n﹣1+n(![]() )n,
)n,
![]() Tn=1(
Tn=1(![]() )2+2(
)2+2(![]() )3+3(
)3+3(![]() )4+…+(n﹣1)(
)4+…+(n﹣1)(![]() )n+n(
)n+n(![]() )n+1,
)n+1,
两式相减可得![]() Tn
Tn![]() (
(![]() )2+(
)2+(![]() )3+(
)3+(![]() )4+…+(
)4+…+(![]() )n﹣n(
)n﹣n(![]() )n+1
)n+1
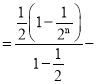 n(
n(![]() )n+1,
)n+1,
化简可得Tn=2﹣(n+2)(![]() )n.
)n.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
(1)求E的方程;
(2)若点A,B是E上的两个动点,O为坐标原点,且![]() ,求证:直线AB恒过定点.
,求证:直线AB恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案①:规定每日底薪50元,快递业务每完成一单提成3元;方案②:规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,整理得到如图所示的频率分布直方图.
七组,整理得到如图所示的频率分布直方图.

(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案①,丙、丁选择了日工资方案②.现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案①的概率;
(3)若从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 组,得到如图所示的频率分布直方图.若尺寸落在区间
组,得到如图所示的频率分布直方图.若尺寸落在区间![]() 之外,则认为该零件属“不合格”的零件,其中
之外,则认为该零件属“不合格”的零件,其中![]() ,
,![]() 分别为样本平均和样本标准差,计算可得
分别为样本平均和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
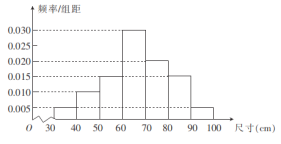
(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前![]() 组中抽出
组中抽出![]() 个零件,标上记号,并从这
个零件,标上记号,并从这![]() 个零件中再抽取
个零件中再抽取![]() 个,求再次抽取的
个,求再次抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若函数![]() 在区间
在区间![]() 内恰有一个零点,求
内恰有一个零点,求![]() 的取值范围;
的取值范围;
(3)设![]() ,当函数
,当函数![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com