
【题目】已知椭圆![]() 过点
过点![]() ,
,![]() 分别为椭圆C的左、右焦点且
分别为椭圆C的左、右焦点且![]() .
.
(1)求椭圆C的方程;
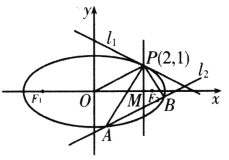
(2)过P点的直线![]() 与椭圆C有且只有一个公共点,直线
与椭圆C有且只有一个公共点,直线![]() 平行于OP(O为原点),且与椭圆C交于两点A、B,与直线
平行于OP(O为原点),且与椭圆C交于两点A、B,与直线![]() 交于点M(M介于A、B两点之间).
交于点M(M介于A、B两点之间).
(i)当![]() 面积最大时,求
面积最大时,求![]() 的方程;
的方程;
(ii)求证:![]() ,并判断
,并判断![]() ,
,![]() 的斜率是否可以按某种顺序构成等比数列.
的斜率是否可以按某种顺序构成等比数列.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;(ii)证明见解析,不可能构成等比数列.
;(ii)证明见解析,不可能构成等比数列.
【解析】
(1)设![]() ,
,![]() .求出
.求出![]() 的坐标,根据
的坐标,根据![]() ,求出
,求出![]() .把点
.把点![]() 代入椭圆方程,结合
代入椭圆方程,结合![]() ,求出
,求出![]() ,即得椭圆C的方程;
,即得椭圆C的方程;
(2)(i)设![]() 方程为
方程为![]() ,
,![]() .把直线
.把直线![]() 的方程代入椭圆方程,由韦达定理、弦长公式求出
的方程代入椭圆方程,由韦达定理、弦长公式求出![]() .由点到直线的距离公式求出点P到
.由点到直线的距离公式求出点P到![]() 的距离
的距离![]() ,则
,则![]() ,根据基本不等式求面积的最大值,即求
,根据基本不等式求面积的最大值,即求![]() 的方程;(ii)要证结论成立,只须证明
的方程;(ii)要证结论成立,只须证明![]() ,即证直线
,即证直线![]() 为
为![]() 的平分线,转化成证明
的平分线,转化成证明![]() .
.
又![]() 与C有一个公共点,即
与C有一个公共点,即![]() 为椭圆的切线,可求
为椭圆的切线,可求![]() ,又
,又![]() .由题意
.由题意![]() ,
,![]() ,
,![]() ,
,![]() 四个数按某种顺序成等比数列,推出矛盾,故不可能构成等比数列.
四个数按某种顺序成等比数列,推出矛盾,故不可能构成等比数列.
(1)设![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
![]() ,
,![]() .
.
又![]() 在椭圆上,故
在椭圆上,故![]() ,
,
又![]() ,解得
,解得![]() ,
,![]() ,
,
故所求方程为![]() .
.
(2)(i)由于![]() ,
,
设![]() 方程为
方程为![]() ,
,![]() .
.
由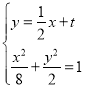 ,消y整理得
,消y整理得![]() ,
,
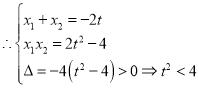 ,
,
则![]()
![]()
![]() .
.
又点P到![]() 的距离
的距离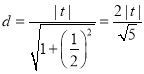 ,
,
![]()
![]()
![]() .
.
当且仅当![]() ,
,![]() ,即
,即![]() 时,等号成立.
时,等号成立.
故直线AB的方程为:![]() .
.
(ⅱ)要证结论成立,只须证明:![]() ,
,
由角平分线性质即证:直线![]() 为
为![]() 的平分线,
的平分线,
转化成证明:![]() .
.
因为![]()
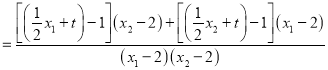
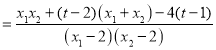
![]()
因此结论成立.
又![]() 与C有一个公共点,即
与C有一个公共点,即![]() 为椭圆的切线,
为椭圆的切线,
由![]() 得
得![]()
令![]() ,
,![]() ,
,
则![]() ,
,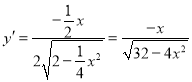
所以![]() ,所以
,所以![]() ,
,
故所研究的4条直线的斜率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若这四个数成等比数列,且其公比记为q,
则应有![]() 或
或![]() ,或
,或![]() .
.
因为![]() 不成立,所以
不成立,所以![]() ,
,
而当![]() 时,
时,![]() ,
,![]() ,
,
此时直线PB与![]() 重合,不合题意,
重合,不合题意,
故![]() ,
,![]() ,PA,PB的斜率无论怎样排序都不可能构成等比数列.
,PA,PB的斜率无论怎样排序都不可能构成等比数列.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某部门在上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,单位:分钟)将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分组,制成频率分布直方图如图所示:
分组,制成频率分布直方图如图所示:


(1)求a的值;
(2)记A表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”试估计A的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的.从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成.如图,在正六棱柱![]() 的三个顶点
的三个顶点![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构,如下图(4)所示,
,就形成了蜂巢的结构,如下图(4)所示,
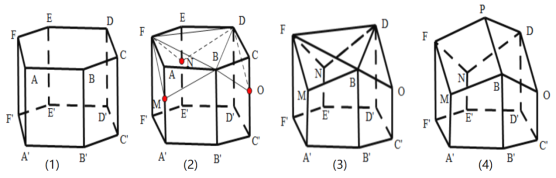
瑞士数学家克尼格利用微积分的方法证明了蜂巢的这种结构是在相同容积下所用材料最省的,英国数学家麦克劳林通过计算得到菱形的一个内角为![]() ,即
,即![]() .以下三个结论①
.以下三个结论①![]() ;②
;② ![]()
![]()
![]() ;③
;③![]() 四点共面,正确命题的个数为______个;若
四点共面,正确命题的个数为______个;若![]() ,
,![]() ,
,![]() ,则此蜂巢的表面积为_______.
,则此蜂巢的表面积为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,….生数皆终,万物复苏,天以更元作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90至100),其余19人的年龄依次相差一岁,则年长者的年龄为( )
A.94B.95C.96D.98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”.整个图形是一个圆形.其中黑色阴影区域在y轴右侧部分的边界为一个半圆,给出以下命题:
①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]()
②当![]() 时,直线y=ax+2a与白色部分有公共点;
时,直线y=ax+2a与白色部分有公共点;
③黑色阴影部分(包括黑白交界处)中一点(x,y),则x+y的最大值为2;
④设点P(﹣2,b),点Q在此太极图上,使得∠OPQ=45°,b的范围是[﹣2,2].
其中所有正确结论的序号是( )

A.①④B.①③C.②④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2),B为抛物线x2=2y﹣2上任意一点,且B为AC的中点,设动点C的轨迹为曲线E.
(1)求曲线E的方程;
(2)是否存在斜率为1的直线l交曲线E于M、N两点,使得△MAN为以MN为底边的等腰三角形?若存在,请求出l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
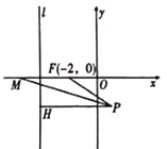
【题目】如图,在平面直角坐标系中,已知点![]() ,直线
,直线![]() ,过动点
,过动点![]() 作
作![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作两条直线,分别交曲线
作两条直线,分别交曲线![]() 于
于![]() 两点(异于
两点(异于![]() 点).当直线
点).当直线![]() 的斜率之和为2时,直线
的斜率之和为2时,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com