
【题目】已知函数f(x)=sin( ![]() ﹣x)sinx﹣
﹣x)sinx﹣ ![]() cos2x. (I)求f(x)的最小正周期和最大值;
cos2x. (I)求f(x)的最小正周期和最大值;
(II)讨论f(x)在[ ![]() ,
, ![]() ]上的单调性.
]上的单调性.
【答案】解:(Ⅰ)函数f(x)=sin( ![]() ﹣x)sinx﹣
﹣x)sinx﹣ ![]() x=cosxsinx﹣
x=cosxsinx﹣ ![]() (1+cos2x) =
(1+cos2x) = ![]() sin2x﹣
sin2x﹣ ![]() cos2x﹣
cos2x﹣ ![]() =sin(2x﹣
=sin(2x﹣ ![]() )﹣
)﹣ ![]() ,
,
故函数的周期为 ![]() =π,最大值为1﹣
=π,最大值为1﹣ ![]() .
.
(Ⅱ)当x∈ ![]() 时,2x﹣
时,2x﹣ ![]() ∈[0,π],故当0≤2x﹣
∈[0,π],故当0≤2x﹣ ![]() ≤
≤ ![]() 时,即x∈[
时,即x∈[ ![]() ,
, ![]() ]时,f(x)为增函数;
]时,f(x)为增函数;
当 ![]() ≤2x﹣
≤2x﹣ ![]() ≤π时,即x∈[
≤π时,即x∈[ ![]() ,
, ![]() ]时,f(x)为减函数.
]时,f(x)为减函数.
【解析】(Ⅰ)由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性和最值求得f(x)的最小正周期和最大值. (Ⅱ)根据2x﹣ ![]() ∈[0,π],利用正弦函数的单调性,分类讨论求得f(x)在
∈[0,π],利用正弦函数的单调性,分类讨论求得f(x)在 ![]() 上的单调性.
上的单调性.
【考点精析】通过灵活运用二倍角的余弦公式,掌握二倍角的余弦公式:![]() 即可以解答此题.
即可以解答此题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中
,其中 ![]() =(2cosx,
=(2cosx, ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R
=(cosx,1),x∈R
(1)求函数y=f(x)的最小正周期和单调递增区间:
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=2,a= ![]() 且sinB=2sinC,求△ABC的面积.
且sinB=2sinC,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
分 组 | 频 数 | 频 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 计 | n | 1 |
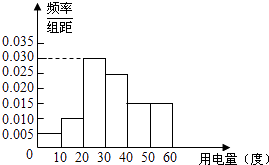
(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某矿山企业生产某产品的年固定成本为![]() 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入![]() 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品![]() 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为![]() 万元,且
万元,且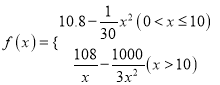
(Ⅰ)写出年利润![]() (万元)关于产品年产量
(万元)关于产品年产量![]() (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)问:年产量![]() 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?
注:年利润=年销售收入-年总成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<π),在同一周期内,当 ![]() 时,f(x)取得最大值3;当
时,f(x)取得最大值3;当 ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(1)求函数f(x)的解析式和图象的对称中心;
(2)若 ![]() 时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com