
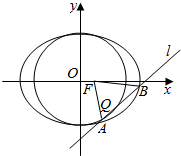
 已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )
已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )| A. | 4 | B. | 1 | C. | 2 | D. | 3 |
分析 设A(x1,y1),(x1>0),连接OA,OQ,则|AQ|2=${x}_{1}^{2}+{y}_{1}^{2}-3$,|AF|2=${{(x}_{1}^{\;}-1)}^{2}+{y}_{1}^{2}$,结合${y}_{1}^{2}=3-\frac{{3{x}_{1}}^{2}}{4}$,化简可得答案.
解答 解:设A(x1,y1),(x1>0),
连接OA,OQ,在△OAQ中,|AQ|2=${x}_{1}^{2}+{y}_{1}^{2}-3$,
∵|AF|2=${{(x}_{1}^{\;}-1)}^{2}+{y}_{1}^{2}$,
又由${y}_{1}^{2}=3-\frac{{3{x}_{1}}^{2}}{4}$得:
|AQ|2=${\frac{1}{4}x}_{1}^{2}$,即|AQ|=$\frac{1}{2}$x1,
|AF|2=${\frac{1}{4}x}_{1}^{2}-2{x}_{1}+4$,即|AF|=2-$\frac{1}{2}$x1,
∴|AF|+|AQ|=2,
故选:C.
点评 本题考查的知识点是椭圆的简单性质,直线与圆锥曲线的关系,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com