
分析 (Ⅰ)依题意,直线l的方程为y=x-1,与椭圆方程联立得2x2-3x=0.设E(x1,y1),F(x2,y2),线段EF的中点为M(x0,y0),利用根与系数的关系、中点坐标公式即可得出.
(Ⅱ)设直线l的方程为x=my+1,与椭圆方程联立(m2+3)y2+2my-2=0,显然m∈R.设E(x1,y1),F(x2,y2),E1(3,y1),F1(3,y2).由λ=S1S2=$\frac{1}{2}(3-{x}_{1})|{y}_{1}|$×$\frac{1}{2}(3-{x}_{2})|{y}_{2}|$=$\frac{1}{4}$$[4-2m({y}_{1}+{y}_{2})+{m}^{2}{y}_{1}{y}_{2}]$|y1y2|,代入根与系数的关系,利用二次函数的单调性即可得出.
解答 解:(Ⅰ)依题意,直线l的方程为y=x-1,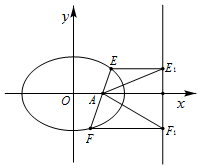
由$\left\{{\begin{array}{l}{y=x-1}\\{{x^2}+3{y^2}-3=0}\end{array}}\right.$,得2x2-3x=0.
设E(x1,y1),F(x2,y2),线段EF的中点为M(x0,y0),则x1+x2=$\frac{3}{2}$,x0=$\frac{3}{4}$,
y0=x0-1=-$\frac{1}{4}$.所以M$(\frac{3}{4},-\frac{1}{4})$.
(Ⅱ)设直线l的方程为x=my+1,由$\left\{{\begin{array}{l}{x=my+1}\\{{x^2}+3{y^2}-3=0}\end{array}}\right.$,
得(m2+3)y2+2my-2=0,显然m∈R.
设E(x1,y1),F(x2,y2),则${y_1}+{y_2}=\frac{-2m}{{{m^2}+3}}$,${y_1}{y_2}=\frac{-2}{{{m^2}+3}}$.
E1(3,y1),F1(3,y2).
因为λ=S1S2=$\frac{1}{2}(3-{x}_{1})|{y}_{1}|$×$\frac{1}{2}(3-{x}_{2})|{y}_{2}|$=$\frac{1}{2}$(2-my1)(2-my2)|y1y2|=$\frac{1}{4}$$[4-2m({y}_{1}+{y}_{2})+{m}^{2}{y}_{1}{y}_{2}]$|y1y2|=$\frac{{2{m^2}+6+2{m^2}-{m^2}}}{{2({m^2}+3)}}•\frac{2}{{{m^2}+3}}$=$\frac{{3{m^2}+6}}{{{{({m^2}+3)}^2}}}$=$-\frac{3}{{{{({m^2}+3)}^2}}}+\frac{3}{{{m^2}+3}}$.
因为$\frac{1}{{{m^2}+3}}∈(0,\frac{1}{3}]$,
所以实数λ的取值范围是$(0,\frac{2}{3}]$.
点评 本题考查了直线与椭圆相交问题、一元二次方程的根与系数的关系、二次函数的单调性、三角形面积计算公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
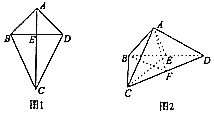 如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.
如图1,四边形ABCD中AC⊥BD,CE=2AE=2BE=2DE=2,将四边形ABCD沿着BD折叠,得到图2所示的三棱锥A-BCD,其中AB⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
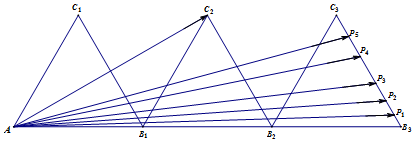
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com