
【题目】是否存在12个集合![]() ,
,![]() ,
,![]() ,
,![]() 和4098个集合
和4098个集合![]() 满足下列三个条件:(1)
满足下列三个条件:(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)当
;(3)当![]() 时,
时,![]() ?
?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,离心率为
,离心率为![]() ,且
,且![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知![]() 为坐标原点,过点
为坐标原点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,若
上,若![]() ,试判断
,试判断![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,现将
,现将![]() 沿
沿![]() 折到
折到![]() 的位置,连结
的位置,连结![]() ,
,![]() ,如图2.
,如图2.
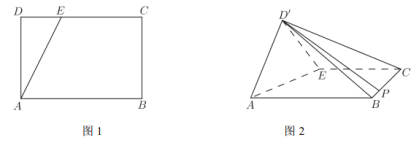
(1)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,证明:
,证明:![]() ;
;
(2)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .若二面角
.若二面角![]() 为
为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为平面上
为平面上![]() 个点的集合,其中任三点不共线,任四点不共圆.一个圆被称为“好圆”是指
个点的集合,其中任三点不共线,任四点不共圆.一个圆被称为“好圆”是指![]() 中有三个点在圆上,
中有三个点在圆上,![]() 个点在圆内,
个点在圆内,![]() 个点在圆外.求证:好圆的个数与
个点在圆外.求证:好圆的个数与![]() 有相同的奇偶性.
有相同的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂共有员工5000人,现从中随机抽取100位员工,对他们每月完成合格产品的件数进行统计,统计表格如下:

(1)工厂规定:每月完成合格产品的件数超过3200件的员工,会被评为“生产能手”称号.由以上统计数据填写下面的![]() 列联表,并判断是否有95%的把握认为“生产能手”称号与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”称号与性别有关?
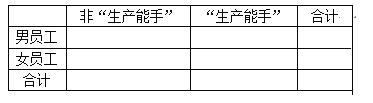
(2)为提高员工劳动的积极性,该工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的(包括2600件),计件单价为1元;超出(0,200]件的部分,累进计件单价为1.2元;超出(200,400]件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段的频率视为相应的概率,在该厂男员工中随机选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)超过3100元的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() ,
,
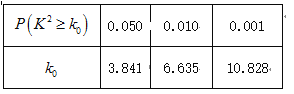
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 丄底面
丄底面![]() .
.
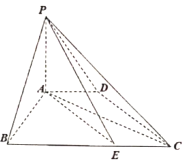
(1)证明:平面![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四棱锥
把四棱锥![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com