已知数列{an}的前n项和为Sn=an-1(a为不为零的实数),则此数列( )
A.一定是等差数列
B.一定是等比数列
C.或是等差数列或是等比数列
D.既不可能是等差数列,也不可能是等比数列
【答案】
分析:由题意可知,当a=1时,a
n-a
n-1=0;当a≠1时,

,所以数列{a
n}或是等差数列或是等比数列.
解答:解:当a=1时,
a
1=a-1=0,
a
n=S
n-S
n-1=(a
n-1)-(a
n-1-1)=0,
a
n-1=S
n-1-S
n-2=(a
n-1-1)-(a
n-2-1)=0,
∴a
n-a
n-1=0,
∴数列{a
n}是等差数列.
当a≠1时,
a
1=a-1,
a
n=S
n-S
n-1=(a
n-1)-(a
n-1-1)=a
n-a
n-1,
a
n-1=S
n-1-S
n-2=(a
n-1-1)-(a
n-2-1)=a
n-1-a
n-2,
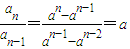
,
∴数列{a
n}是等比数列.
综上所述,数列{a
n}或是等差数列或是等比数列.
故选C.
点评:本题考查数列的概念,解题时要注意a=0的情况,避免丢解.

 ,所以数列{an}或是等差数列或是等比数列.
,所以数列{an}或是等差数列或是等比数列.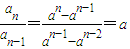 ,
,

 阅读快车系列答案
阅读快车系列答案