
【题目】已知等比数列{an}的公比q>1,且a1+a3=20,a2=8. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,Sn是数列{bn}的前n项和,对任意正整数n不等式
,Sn是数列{bn}的前n项和,对任意正整数n不等式 ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】解:(Ⅰ)设数列{an}的公比为q,a1+a3=20,a2=8.
则 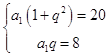 ,
,
∴2q2﹣5q+2=0
∵公比q>1,∴ ![]() ,∴数列{an}的通项公式为
,∴数列{an}的通项公式为 ![]() .
.
(Ⅱ)解:∴ ![]()
![]() Sn=
Sn= ![]()
∴ ![]()
∴Sn= ![]() =
= 
∴ ![]() 对任意正整数n恒成立,设
对任意正整数n恒成立,设 ![]() ,易知f(n)单调递增.
,易知f(n)单调递增.
n为奇数时,f(n)的最小值为 ![]() ,∴
,∴ ![]() 得
得 ![]() ,
,
n为偶数时,f(n)的最小值为 ![]() ,∴
,∴ ![]() ,
,
综上, ![]() ,即实数a的取值范围是
,即实数a的取值范围是 ![]() .
.
【解析】(Ⅰ)设数列{an}的公比为q,l利用a1+a3=20,a2=8.列出方程组,求出首项与公比然后求解通项公式.(Ⅱ)利用错位相减法求和求出Sn,∴ ![]() 对任意正整数n恒成立,设
对任意正整数n恒成立,设 ![]() ,f(n)单调递增.通过n为奇数时,n为偶数时,分别f(n)的最小值,求解实数a的取值范围.
,f(n)单调递增.通过n为奇数时,n为偶数时,分别f(n)的最小值,求解实数a的取值范围.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系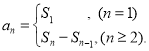 ).
).


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知正三角形ABC的边长为2,AM是边BC上的高,沿AM将△ABM折起,使得二面角B﹣AM﹣C的大小为90°,此时点M到平面ABC的距离为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学有刘徽发现当圆内接多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.某同学利用刘徽的“割圆术”思想设计了一个计算圆周率的近似值的程序框图如图,则输出S的值为 (参考数据:sin15°=0.2588,sin7.5°=0.1305)( )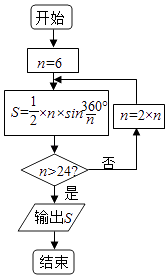
A.2.598
B.3.106
C.3.132
D.3.142
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别是a,b,c且满足(2a﹣c)cosB=bcosC,
(1)求角B的大小;
(2)若△ABC的面积为为 ![]() 且b=
且b= ![]() ,求a+c的值.
,求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(3x+ ![]() ).
).
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,f( ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,求cosα﹣sinα的值.
)cos2α,求cosα﹣sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: 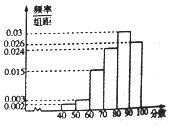
(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a、b、c分别是△ABC的三个内角A、B、C的对边.
(1)若△ABC面积S△ABC= ![]() ,c=2,A=60°,求a、b的值;
,c=2,A=60°,求a、b的值;
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com