
【题目】【2017长沙模拟】如图,在直棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=![]() ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.
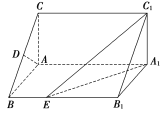
(1)求证:AD⊥C1E;
(2)当异面直线AC,C1E所成的角为60°时,求三棱锥C1A1B1E的体积.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】 (1)证明:因为AB=AC,D是BC的中点,所以AD⊥BC.①
又在直三棱柱ABCA1B1C1中,BB1⊥平面ABC,
而AD平面ABC,所以AD⊥BB1.②
由①②得AD⊥平面BB1C1C.
由点E在棱BB1上运动,得C1E平面BB1C1C,所以AD⊥C1E.
(2)因为AC∥A1C1,所以∠A1C1E是异面直线AC,C1E所成的角,由题设,∠A1C1E=60°.
因为∠B1A1C1=∠BAC=90°,所以A1C1⊥A1B1,又AA1⊥A1C1,从而A1C1⊥平面A1ABB1,
于是A1C1⊥A1E. 故C1E=![]() =2
=2![]() ,又B1C1=
,又B1C1=![]() =2,
=2,
所以B1E=![]() =2,从而V三棱锥C1A1B1E=
=2,从而V三棱锥C1A1B1E=![]() S△A1B1E×A1C1=
S△A1B1E×A1C1=![]() ×
×![]() ×2×
×2×![]() ×
×![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
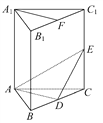
【题目】如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1.
(2)直线A1F∥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司从1999年的年产值100万元,增加到10年后2009年的500万元,如果每年产值增长率相同,则每年的平均增长率是多少?(ln(1+x)≈x,lg2=0.3,ln10=2.30)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017兰州高考模拟】.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
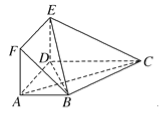
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲![]() 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为![]() 万元,且
万元,且![]() (
(![]() ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为![]() (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;
(2)为了让年利润![]() 不低于2360万元,求年产量
不低于2360万元,求年产量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-3x+2≤0},集合B={y|y=x2-2x+a},集合C={x|x2-ax-4≤0}.命题p:A∩B≠;命题q:AC.
(1)若命题p为假命题,求实数a的取值范围;
(2)若命题p∧q为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,其中
,其中![]() 为坐标原点,判断
为坐标原点,判断![]() 到直线
到直线![]() 的距离是否为定值?若是,求出该定值;若不是,请说明理由.
的距离是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com