
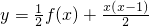 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;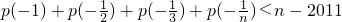 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由. -2x+1,由切线方程知f′(1)=1,∴a=2,
-2x+1,由切线方程知f′(1)=1,∴a=2,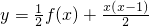 =lnx,它的反函数为p(x)=ex,
=lnx,它的反函数为p(x)=ex,

 +
+ +
+ +…+
+…+
 )+(1-
)+(1- )+(1-
)+(1- )+…(1-
)+…(1- )
) +
+ +
+ +…+
+…+ )≈n-ln(n+1)+C(C=0.57722…一个无理数,称作欧拉初始)
)≈n-ln(n+1)+C(C=0.57722…一个无理数,称作欧拉初始)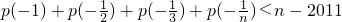 恒成立.
恒成立.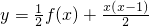 =lnx,它的反函数为p(x)=ex,求其导数,利用导数大于0原函数是增函数,导数小于0原函数是减函数,进而求出函数t(x)的最大值.
=lnx,它的反函数为p(x)=ex,求其导数,利用导数大于0原函数是增函数,导数小于0原函数是减函数,进而求出函数t(x)的最大值. ,将原不等式转化成不等式n-(
,将原不等式转化成不等式n-( +
+ +
+ +…+
+…+ )<n-2010,利用调和级数的和,从而得到取N=[e2010+C],当n>N时,不等式
)<n-2010,利用调和级数的和,从而得到取N=[e2010+C],当n>N时,不等式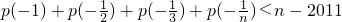 恒成立.
恒成立.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com