
【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为: ![]() .估计该校学生每周平均体育运动时间超过4小时的概率;
.估计该校学生每周平均体育运动时间超过4小时的概率;

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附: 
【答案】(1)90(2)0.75(3)有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
【解析】试题分析:(1)![]() 应收集
应收集![]() 位女生的样本数据;(2)由图得每周平均体育运动超过
位女生的样本数据;(2)由图得每周平均体育运动超过![]() 小时的频率为
小时的频率为![]() 该校学生每周平均体育运动时间超过
该校学生每周平均体育运动时间超过![]() 小时的概率的估计值为
小时的概率的估计值为![]() ;(3)求出列联表代入公式可得
;(3)求出列联表代入公式可得![]() 有
有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
试题解析: (1)![]() ,所以应收集
,所以应收集![]() 位女生的样本数据;
位女生的样本数据;
(2)由频率分布直方图得每周平均体育运动超过![]() 小时的频率为
小时的频率为![]() ,所以该校学生每周平均体育运动时间超过
,所以该校学生每周平均体育运动时间超过![]() 小时的概率的估计值为
小时的概率的估计值为![]() ;
;
(3)由(2)知,![]() 位学生有
位学生有![]() (位)的每周平均体育运动时间超过
(位)的每周平均体育运动时间超过![]() 小时,
小时,![]() 人的每周平均体育运动时间不超过
人的每周平均体育运动时间不超过![]() 小时,又因为样本数据中有
小时,又因为样本数据中有![]() 份是关于男生的,
份是关于男生的,![]() 份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过 |
|
|
|
每周平均体育运动时间超过 |
|
|
|
总计 |
|
|
|
结合列联表可算得![]() ,
,
所以有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.


科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.

(1)若AP⊥AQ,证明:直线PQ过定点,并求出定点的坐标;
(2)假设直线PQ过点T(5,-2),请问是否存在以PQ为底边的等腰三角形APQ?若存在,求出△APQ的个数,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
, ![]() ,
, ![]() ,若
,若![]() 为
为![]() 的中点,且
的中点,且![]() .
.
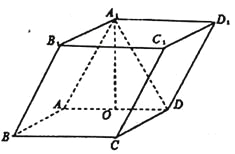
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-3|-|x+1|,x∈R.
(1)解不等式f(x)<-1;
(2)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
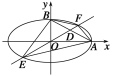
(1)若![]() =6
=6![]() ,求k的值;
,求k的值;
(2)求四边形AEBF面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为![]() ,宽为
,宽为![]() 的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转
的长方形铁皮做一个无盖的容器.先在四角分别截去一个小正方形,然后把四边翻转![]() ,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?
,再焊接而成(如图).问该容器的高为多少时,容器的容积最大?最大容积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com