
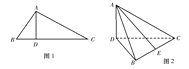
【题目】如图1,在Rt△ABC中,∠ABC=60°,∠BAC=90°,AD是BC边上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
(1)证明:平面ABD⊥平面BCD;
(2)设E为BC的中点,BD=2,求异面直线AE与BD所成的角的大小.
【答案】(1)见解析(2)异面直线AE与BD所成的角的大小为60°.
【解析】试题分析:(1)由折叠可知AD⊥CD,AD⊥BD,再根据线面垂直判定定理得AD⊥平面BCD.最后根据面面垂直判定定理得结论(2)线线角找平行:取CD的中点F,则结合三角形中位线性质得∠AEF为异面直线AE与BD所成的角,最后通过解三角形得异面直线AE与BD所成的角的大小
试题解析:(1)因为折起前AD是BC边上的高,
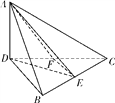
则当△ABD折起后,AD⊥CD,AD⊥BD
又CD∩BD=D,则AD⊥平面BCD.
因为AD平面ABD,所以平面ABD⊥平面BCD.
(2)取CD的中点F,连接EF,则EF∥BD,
所以∠AEF为异面直线AE与BD所成的角.
连结AF、DE.由BD=2,则EF=1,AD=2![]() ,CD=6,DF=3.
,CD=6,DF=3.
在Rt△ADF中,AF=![]() =
=![]() .
.
在△BCD中,由题设∠BDC=60°,则
BC2=BD2+CD2-2BD·CDcos∠BDC=28,即BC=2![]() ,
,
从而BE=![]() BC=
BC=![]() ,cos∠CBD=
,cos∠CBD=![]() =-
=-![]() .
.
在△BDE中,DE2=BD2+BE2-2BD·BEcos∠CBD=13.
在Rt△ADE中,AE=![]() =5.
=5.
在△AEF中,cos∠AEF=![]() =
=![]() .
.
所以异面直线AE与BD所成的角的大小为60°.


科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(I)求直方图中![]() 的值;
的值;
(II)求月平均用电量的众数和中位数;
(III)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取![]() 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,由此得到样本的重量频率分布直方图(如图).
,由此得到样本的重量频率分布直方图(如图).

(Ⅰ)求![]() 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(Ⅱ)从盒子中随机抽取![]() 个小球,其中重量在
个小球,其中重量在![]() 内的小球个数为
内的小球个数为![]() ,求
,求![]() 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(![]() )班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.
)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.

(1)求全班人数及分数在![]() 之间的频数,并估计该班的平均分数;
之间的频数,并估计该班的平均分数;
(2)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
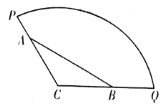
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学校食堂的服务情况,随机调查了50名就餐的教师和学生.根据这50名师生对餐厅服务质量进行评分,绘制出了频率分布直方图(如图所示),其中样本数据分组为![]() .
.
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的师生中,随机抽取2人,求此人中恰好有1人评分在
的师生中,随机抽取2人,求此人中恰好有1人评分在![]() 上的概率;
上的概率;
(3)学校规定:师生对食堂服务质量的评分不得低于75分,否则将进行内部整顿,试用组中数据估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二数学期中测试中,为了了解学生的考试情况,从中抽取了![]() 个学生的成绩(满分为100分)进行统计.按照[50,60), [60,70), [70,80), [80,90), [90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60), [90,100]的数据).
个学生的成绩(满分为100分)进行统计.按照[50,60), [60,70), [70,80), [80,90), [90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60), [90,100]的数据).

(1)求样本容量![]() 和频率分布直方图中
和频率分布直方图中![]() 的值;
的值;
(2)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取3名参加志愿者活动,所抽取的3名同学中至少有一名成绩在[90,100]内的概率。.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如下表:
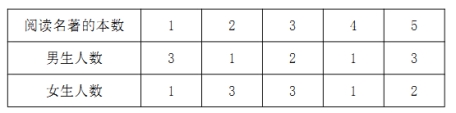
(1)试根据上述数据,求这个班级女生阅读名著的平均本数;
(2)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率;
(3)试比较该班男生阅读名著本数的方差![]() 与女生阅读名著本数的方差
与女生阅读名著本数的方差![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求适合下列条件的直线方程:
(1)经过点P(3,2)且在两坐标轴上的截距相等;
(2)经过点A(-1,-3),倾斜角等于直线y=3x的倾斜角的2倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com