
【题目】已知函数f(x)= ![]() (a是常数,且a>0).对于下列命题:①函数f(x)的最小值是﹣1;②函数f(x)在R上是单调函数;③若f(x)>0在[
(a是常数,且a>0).对于下列命题:①函数f(x)的最小值是﹣1;②函数f(x)在R上是单调函数;③若f(x)>0在[ ![]() ,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2 , 恒有f(
,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2 , 恒有f( ![]() )>
)> ![]() .其中正确命题的序号是( )
.其中正确命题的序号是( )
A.①②
B.①③
C.③④
D.②④
【答案】B
【解析】解:函数f(x)= ![]() (a是常数,且a>0)的图象如下图所示:
(a是常数,且a>0)的图象如下图所示: 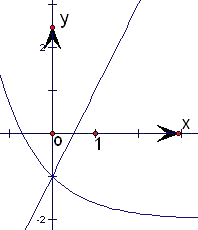
① 由图可得:当x=0时,函数f(x)的最小值是﹣1;故正确;②由图象说明函函数f(x)在R上不是单调函数;故错;③若f(x)>0在[ ![]() ,+∞)上恒成立,则f(
,+∞)上恒成立,则f( ![]() )=a﹣1>0,求得a的取值范围是a>1;故正确;④已知函数函数在(﹣∞,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,即f(
)=a﹣1>0,求得a的取值范围是a>1;故正确;④已知函数函数在(﹣∞,0)上的图象在[0,+∞)上是下凹的,所以任取两点连线应在图象的上方,即f( ![]() )<
)< ![]() ,故错误.故正确命题的序号是:①③.故选:B
,故错误.故正确命题的序号是:①③.故选:B
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】【选修4—4:坐标系与参数方程】
将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线![]() 与C的交点为
与C的交点为![]() ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=ln ![]() 的图象分别与直线y=m交于A,B两点,则|AB|的最小值为( )
的图象分别与直线y=m交于A,B两点,则|AB|的最小值为( )
A.2
B.2+ln2
C.e2 ![]()
D.2e﹣ln ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个集合U,A,B及元素间的关系如图所示,则(CUA)∩B=( ) 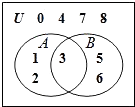
A.{5,6}
B.{3,5,6}
C.{3}
D.{0,4,5,6,7,8}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
分 组 | 频 数 | 频 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 计 | n | 1 |

(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com