
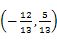 ,θ为a与b的夹角.
,θ为a与b的夹角.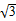 sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间.  期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:不详 题型:解答题
 cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+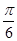 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n.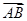 ·
·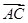 =
= ,求边BC的最小值.
,求边BC的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
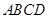 中,
中,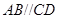 ,
,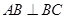 ,
,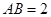 ,
,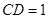 ,
,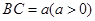 ,P为线段
,P为线段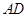 (含端点)上一个动点,设
(含端点)上一个动点,设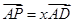 ,
,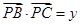 ,对于函数
,对于函数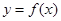 ,给出以下三个结论:①当
,给出以下三个结论:①当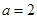 时,函数
时,函数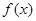 的值域为
的值域为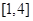 ;②对任意
;②对任意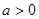 ,都有
,都有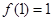 成立;③对任意
成立;③对任意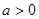 ,函数
,函数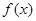 的最大值都等于4.④存在实数
的最大值都等于4.④存在实数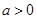 ,使得函数
,使得函数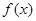 最小值为0 .其中所有正确结论的序号是_________.
最小值为0 .其中所有正确结论的序号是_________.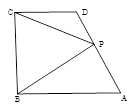
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
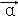 和
和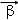 ,定义
,定义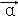 ○
○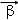 =
=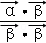 ,若平面向量
,若平面向量 、
、 满足|
满足| |≥|
|≥| |>0,
|>0, 与
与 的夹角
的夹角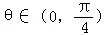 ,且
,且 ○
○ 和
和 ○
○ 都在集合
都在集合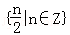 中,则
中,则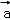 ○
○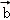 =( )
=( )A.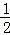 | B.1 | C.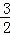 | D.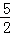 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
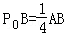 ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有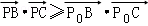 则( )
则( )| A.∠ABC=90° | B.∠BAC=90° | C.AB=AC | D.AC=BC |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
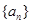 是公比为
是公比为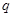 的无穷等比数列,下列
的无穷等比数列,下列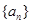 的四组量中,一定能成为该数列“基本量”的是第 组;
的四组量中,一定能成为该数列“基本量”的是第 组;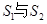 ;②
;②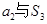 ;③
;③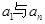 ;④
;④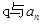 .
. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com