
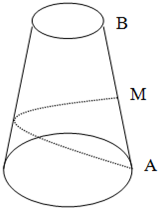
如图,圆台上底半径为1,下底半径为4,母线AB=18,从AB中点M拉一条绳子绕圆台侧面转到A点。
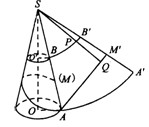
(1)求绳子的最短长度;
(2)求绳子最短时,上底圆周上的点到绳子的最短距离。
(1)21;(2)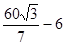
【解析】
试题分析: (1)要求绳子AM绕圆台一周的最短长度,则可沿AB将圆台的曲面展开,得扇环面(即将曲面问题转化为平面问题),然后求出扇环面上AM’间的距离,AM’=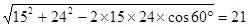 ,即绳子的最短长度为21。
,即绳子的最短长度为21。
(2)要研究此时上底圆周上的点到绳子的最短距离,则需将扇环补充成扇形,这样将BB’上的点到AM’的最短距离问题转化为点S到AM’的最短距离(因为点S到BB’上的点的距离等于半径SB)。故只需求出S到AM’的距离SQ,再减去半径SP即可。即上底圆周上的点到绳子最短距离PQ=SQ-SP=SQ-SB=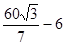 。
。
考点:本题主要考查圆台的几何特征及其展开图、距离的计算。
点评:此题用到将圆台“补成”圆锥再展开进行研究,这种割、补、拼凑的思想,是重要的数学思维方法。


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
 如图,圆台上底半径为1,下底半径为4,母线AB=18;从AB的中点M拉一条绳子绕圆台侧面转到点A,则绳子的最短长度为
如图,圆台上底半径为1,下底半径为4,母线AB=18;从AB的中点M拉一条绳子绕圆台侧面转到点A,则绳子的最短长度为60
| ||
| 7 |
60
| ||
| 7 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
有上底面半径2,下底面半径6,高为4的圆台,挖去一个以圆台上底面为底,高为4的圆柱,得到如图所示的几何体,如果用一个与圆台下底面距离等于2并且平行底面的平面去截它,求所得截面的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
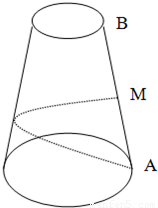
 如图,圆台上底半径为1,下底半径为4,母线AB=18;从AB的中点M拉一条绳子绕圆台侧面转到点A,则绳子的最短长度为________当绳子最短时,上底圆周上的点到绳子的最短距离为________.
如图,圆台上底半径为1,下底半径为4,母线AB=18;从AB的中点M拉一条绳子绕圆台侧面转到点A,则绳子的最短长度为________当绳子最短时,上底圆周上的点到绳子的最短距离为________.查看答案和解析>>
科目:高中数学 来源:2012年湖北省黄冈中学高三适应性考试数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com