
【题目】如图,已知点P在圆柱![]() 的底面圆
的底面圆![]() 上,AB为圆
上,AB为圆![]() 的直径,圆柱
的直径,圆柱![]() 的表面积为20π,
的表面积为20π,![]()
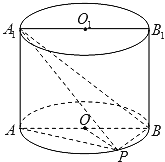
(1)求异面直线![]() 与AP所成角的大小(结果用反三角函数值表示);
与AP所成角的大小(结果用反三角函数值表示);
(2)求点A到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线上一动点P(x,y)(x>0)到定点F(![]() ,0)的距离与它到直线l:x
,0)的距离与它到直线l:x![]() 的距离的比是
的距离的比是![]() .
.
(1)求动点P的轨迹E的方程;
(2)若M是曲线E上的一个动点,直线l′:y=x+4,求点M到直线l′的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,右顶点为B,且满足
,右顶点为B,且满足![]()
![]() Ⅰ
Ⅰ![]() 求椭圆的离心率e;
求椭圆的离心率e;
![]() Ⅱ
Ⅱ![]() 设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点
设P为椭圆上异于顶点的点,以线段PB为直径的圆经过点![]() ,问是否存在过
,问是否存在过![]() 的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二阶方矩阵![]() ,则矩阵
,则矩阵![]() 所对应的矩阵变换为:
所对应的矩阵变换为:![]() ,其意义是把点
,其意义是把点![]() 变换为点
变换为点![]() ,矩阵
,矩阵![]() 叫做变换矩阵.
叫做变换矩阵.
(1)当变换矩阵![]() 时,点
时,点![]() 、
、![]() 经矩阵变换后得到点分别是
经矩阵变换后得到点分别是![]() 、
、![]() ,求经过点
,求经过点![]() 、
、![]() 的直线的点方向式方程;
的直线的点方向式方程;
(2)当变换矩阵![]() 时,若直线上的任意点
时,若直线上的任意点![]() 经矩阵变换后得到的点
经矩阵变换后得到的点![]() 仍在该直线上,求直线的方程;
仍在该直线上,求直线的方程;
(3)若点![]() 经过矩阵
经过矩阵![]() 变换后得到点
变换后得到点![]() ,且
,且![]() 与
与![]() 关于直线
关于直线![]() 对称,求变换矩阵
对称,求变换矩阵![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的AQI指数M与当天的空气水平可见度![]() (单位:cm)的情况如表1:
(单位:cm)的情况如表1:
| 900 | 700 | 300 | 100 |
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年11月份AQI指数频数分布如表2:
|
|
|
|
|
|
频数(天) | 3 | 6 | 12 | 6 | 3 |
<>(1)设
(2)小李在该市开了一家洗车店,洗车店每天的平均收入与AQI指数存在相关关系如表3:
|
|
|
|
|
|
日均收入(元) | -2000 | -1000 | 2000 | 6000 | 8000 |
根据表3估计小李的洗车店2017年11月份每天的平均收入.
附参考公式:![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4坐标系与参数方程选讲
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为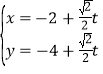 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的平面直角坐标方程和直线
的平面直角坐标方程和直线![]() 的普通方程:
的普通方程:
(2)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com