
 的最小值是-2,求实数a的值,并求出此时f(x)的最大值.
的最小值是-2,求实数a的值,并求出此时f(x)的最大值. 则t∈[0,1],问题转化为二次函数闭区间上的最小值问题,通过分类
则t∈[0,1],问题转化为二次函数闭区间上的最小值问题,通过分类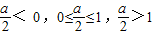 ,分别利用f(x)的最小值是-2,求实数a的值.
,分别利用f(x)的最小值是-2,求实数a的值.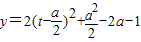 ,t∈[0,1]
,t∈[0,1]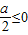 ,即a≤0时,
,即a≤0时,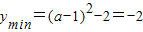 ,故a=1(舍)
,故a=1(舍)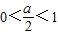 ,即0<a<2时,
,即0<a<2时,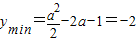
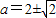 ,取
,取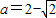 ,此时ymax=-1
,此时ymax=-1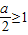 ,即a≥2时,
,即a≥2时,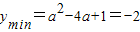
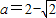 时ymax=-1;当a=3时ymax=2
时ymax=-1;当a=3时ymax=2

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三摸底考试理科数学 题型:解答题
已知函数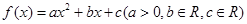 ,若函数
,若函数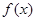 的最小值是
的最小值是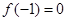 ,且
,且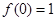 ,对称轴是
,对称轴是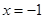 ,
,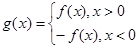 .
.
(1)求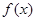 的解析式;
的解析式;
(2)求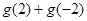 的值;
的值;
(3)在(1)的条件下求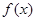 在区间
在区间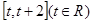 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源:2012届四川省绵阳市高二上学期期末教学质量测试数学试题 题型:选择题
若函数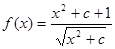 的最小值是2,则实数
的最小值是2,则实数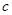 的取值范围是
的取值范围是
A.c≤1 B.c≥1 C.c<0 D.c∈R
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com