
【题目】某校高三年级50名学生参加数学竞赛,根据他们的成绩绘制了如图所示的频率分布直方图,已知分数在![]() 的矩形面积为
的矩形面积为![]() ,
,

求:![]() 分数在
分数在![]() 的学生人数;
的学生人数;
![]() 这50名学生成绩的中位数
这50名学生成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 若分数高于60分就能进入复赛,从不能进入复赛的学生中随机抽取两名,求两人来自不同组的概率.
若分数高于60分就能进入复赛,从不能进入复赛的学生中随机抽取两名,求两人来自不同组的概率.
【答案】(1)3人; (2)76.7; (3)![]() .
.
【解析】
(1)由所有的矩形面积和为1可得:分数在[50,60)的频率为0.06,即可求出;
(2)由0.040+0.06+0.2=0.3,故中位数落在第四组,则中位数为70![]() 10;
10;
(3)分数在[40,50)的有2人,记为a,b,在[50,60)共有3人,记为c,d,e,由此利用列举法能求出从分数[40,60)的5名学生任选2人,两人来自不同组的概率.
![]() 由所有的矩形面积和为1可得:分数在
由所有的矩形面积和为1可得:分数在![]() 的频率为
的频率为![]() ,故分数在
,故分数在![]() 的人数是
的人数是![]() 人,
人,
![]() 由
由![]() ,
,
故中位数落在第四组,
则中位数为![]()
![]() 分数在
分数在![]() 的有2人,记为a,b,在
的有2人,记为a,b,在![]() 共有3人,记为c,d,e,
共有3人,记为c,d,e,
从分数在![]() 的5名学生任选2人的方法有:ab、ac、ad、ae、bc、bd、be、cd、ce、de,共10种,
的5名学生任选2人的方法有:ab、ac、ad、ae、bc、bd、be、cd、ce、de,共10种,
两人来自不同组的有ac、ad、ae、bc、bd、be共6种,
![]() 两人来自不同组的概率
两人来自不同组的概率![]()


科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 轨迹为曲线
轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上关于
上关于![]() 轴对称的两点,点
轴对称的两点,点![]() ,直线
,直线![]() 交曲线
交曲线![]()
于另一点![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
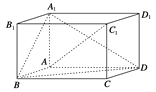
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行文科、理科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.

(Ⅰ)根据数学成绩的频率分布表,求理科数学成绩的中位数的估计值;(精确到0.01)
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:

参考公式与临界值表: 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(![]() ,0),求θ的最小值.
,0),求θ的最小值.
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在梯形
,在梯形![]() 中,
中, ![]() 于
于![]() ,
, ![]()
![]() .将
.将![]() 沿
沿![]() 折起至
折起至![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2),
(如图2), ![]() 为线段
为线段![]() 上一点.
上一点.

图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为线段
为线段![]() 中点,求多面体
中点,求多面体![]() 与多面体
与多面体![]() 的体积之比;
的体积之比;
(Ⅲ)是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长.若不存在,请说明理由.
的长.若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com