
【题目】已知函数y=f(x)是定义在[0,2]上的增函数,且图像是连续不断的曲线,若f(0)=M,f(2)=N(M>0,N>0),那么下列四个命题中是真命题的有( )
A.必存在x∈[0,2],使得f(x)![]() B.必存在x∈[0,2],使得f(x)
B.必存在x∈[0,2],使得f(x)![]()
C.必存在x∈[0,2],使得f(x)![]() D.必存在x∈[0,2],使得f(x)
D.必存在x∈[0,2],使得f(x)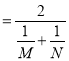
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,设点A(-3,0),B(3,0),直线AM,BM相交于点M,且它们的斜率之积是![]()
(1)试讨论点M的轨迹形状;
(2)当0<b<3时,若点M的轨迹上存在点P(P在x轴的上方),使得∠APB=120°,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市经营一批产品,在市场销售中发现此产品在30天内的日销售量P(件)与日期![]() )之间满足
)之间满足![]() ,已知第5日的销售量为55件,第10日的销售量为50件。
,已知第5日的销售量为55件,第10日的销售量为50件。
(1)求第20日的销售量; (2)若销售单价Q(元/件)与![]() 的关系式为
的关系式为![]() ,求日销售额
,求日销售额![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形![]() 如图(1)所示,其中
如图(1)所示,其中![]() ,
, ![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,现沿
的正方形,现沿![]() 进行折叠,使得平面
进行折叠,使得平面![]() 平面
平面![]() ,得到如图(2)所示的几何体.
,得到如图(2)所示的几何体.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,整理得到数据分组及频率分布表和频率分布直方图:
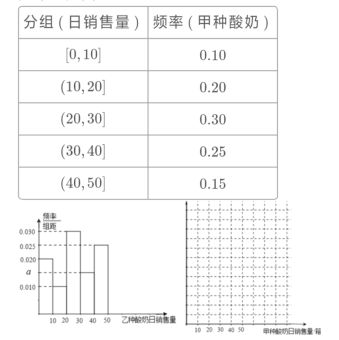
(1)写出频率分布直方图中![]() 的值,并做出甲种酸奶日销售量的频率分布直方图;
的值,并做出甲种酸奶日销售量的频率分布直方图;
(2)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() 。试比较
。试比较![]() 和
和![]() 的大小
的大小
(3)假设同一组中的每个数据可用该组区间的中间值代替,试估计乙种酸奶在未来一个月(按30天计算)的销售总量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱台![]() 中,上底面边长为4,下底面边长为8,高为5,点
中,上底面边长为4,下底面边长为8,高为5,点![]() 分别在
分别在![]() 上,且
上,且![]() .过点
.过点![]() 的平面
的平面![]() 与此四棱台的下底面会相交,则平面
与此四棱台的下底面会相交,则平面![]() 与四棱台的面的交线所围成图形的面积的最大值为
与四棱台的面的交线所围成图形的面积的最大值为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com