练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    方程-log3x=x+2的根所在的区间为


    1. A.
      （0，1）
    2. B.
      （1，2）
    3. C.
      （2，3）
    4. D.
      （3，4）
    A
    分析：构建函数，确定函数的定义域，求导函数，判断函数在定义域上为单调增函数，再用零点存在定理判断即可．
    解答：构建函数f（x）=x+2+log3x，则函数的定义域为（0，+∞）
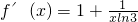
    求导函数，则f′（x）＞0
    ∴函数在（0，+∞）上单调增
    ∵f（1）＞0，x→0，f（x）→-∞
    ∴f（x）=x+2+log3x的零点所在区间为（0，1）
    ∴方程-log3x=x+2的根所在的区间为（0，1）
    故选A．
    点评：本题考查方程与函数之间的联系，考查零点存在定理的运用，同时考查利用导数研究函数的单调性．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    7、方程log3x+x=3的解所在的区间是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    14、若方程log3x+x=3的解所在的区间是（k，k+1），则整数k=
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    9、若方程log3x+x=3的解在区间（n，n+1）内，n∈N，则n的值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    10、方程log3x=-x+3的解所在的区间是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    方程log3x+x=3的解在区间（n，n+1）内，n∈N*，则n=
    2
    2
    ．

    查看答案和解析>>

    同步练习册答案