
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,若对任意的m,
,若对任意的m,![]() ,
,![]() ,都有
,都有![]() .
.
![]() 若
若![]() ,求a的取值范围.
,求a的取值范围.
![]() 若不等式
若不等式![]() 对任意
对任意![]() 和
和![]() 都恒成立,求t的取值范围.
都恒成立,求t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由函数的单调性的定义,构造出f(x)在定义域[﹣5,5],上是增函数,通过增函数性质解不等式得a的取值范围;
(2)由f(x)单调递增且奇函数,利用其最大值整理得关于a,t 的不等式,由a∈[﹣3,0]都恒成立,根据单调性可以求t的取值范围.
解:设任意x1,x2满足﹣5≤x1<x2≤5,由题意可得:
f(x1)﹣f(x2)![]() 即f(x1)<f(x2).所以f(x)在定义域[﹣5,5],上是增函数,
即f(x1)<f(x2).所以f(x)在定义域[﹣5,5],上是增函数,
由f(2a﹣1)<f(3a﹣3),得 ,解得2<a
,解得2<a![]() ,
,
故a的取值范围为(2,![]() ];
];
(2)由以上知f(x)是定义在[﹣5,5]上的单调递增的奇函数,且f(﹣5)=﹣2,
得在[﹣5,5]上f(x)max=f(5)=﹣f(﹣5)=2.
在[﹣5,5]上不等式f(x)≤(a﹣2)t+5对a∈[﹣3,0]都恒成立,
所以2≤(a﹣2)t+5即at﹣2t+3≥0,对a∈[﹣3,0]都恒成立,
令g(a)=at﹣2t+3,a∈[﹣3,0],则只需![]() ,即
,即![]() .
.
解得t![]()
故t的取值范围(﹣∞,![]() ].
].


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】观察下列方程,并回答问题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;…
;…
(1)请你根据这列方程的特点写出第![]() 个方程;
个方程;
(2)直接写出第2009个方程的根;
(3)说出这列方程的根的一个共同特点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.
(Ⅰ)求证:平面BED⊥平面ABCD;
(Ⅱ)求平面PBA与平面EBD所成二面角(锐角)的余弦值.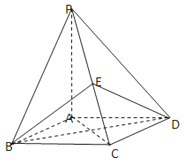
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某中学为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识的竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐、规定:每场知识竞赛前三名的得分都分别为![]() (
(![]() ,且
,且![]() );选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
);选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,则下列推理正确的是( )
A. 每场比赛第一名得分![]() 为4 B. 甲可能有一场比赛获得第二名
为4 B. 甲可能有一场比赛获得第二名
C. 乙有四场比赛获得第三名 D. 丙可能有一场比赛获得第一名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
(Ⅰ)△PBD∽△CBP;
(Ⅱ)AP∥FE.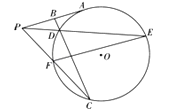
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={y|y=2x+1},B={x|lnx<0},则(UA)∩B=( )
A.?
B.{x|![]() <x≤1}
<x≤1}
C.{x|x<1}
D.{x|0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且a2=8,S4=40.数列{bn}的前n项和为Tn , 且Tn﹣2bn+3=0,n∈N* .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=![]() , 求数列{cn}的前n项和Pn .
, 求数列{cn}的前n项和Pn .
查看答案和解析>>
科目:高中数学 来源: 题型:
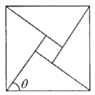
【题目】2002年北京国际数学家大会会标,是以中国古代数学家赵爽的弦图为基础而设计的,弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形![]() 如图
如图![]() ,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为
,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为![]() ,则
,则![]() 等于
等于![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com