
【题目】已知直棱柱ABC﹣A1B1C1中,AC=BC=CC1= ![]() AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
AB,E是线段CC1的中点,连接AE,B1E,AB1 , B1C,BC1 , 得到的图形如图所示. (Ⅰ)证明BC1⊥平面AB1C;
(Ⅱ)求二面角E﹣AB1﹣C的大小.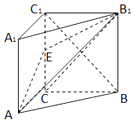
【答案】证明:(Ⅰ)∵直棱柱ABC﹣A1B1C1中,AC=BC=CC1= ![]() AB, ∴AC2+BC2=AB2 , ∴AC⊥BC,
AB, ∴AC2+BC2=AB2 , ∴AC⊥BC,
以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
设AC=BC=CC1= ![]() AB=1,
AB=1,
则B(0,1,0),C1(0,0,1),A(1,0,0),B1(0,1,1),C(0,0,0),![]() =(0,﹣1,1),
=(0,﹣1,1), ![]() =(﹣1,1,1),
=(﹣1,1,1), ![]() =(﹣1,0,0),
=(﹣1,0,0), ![]() =(﹣1,0,1),
=(﹣1,0,1),
∴ ![]()
![]() =0,
=0, ![]() =0﹣1+1=0,
=0﹣1+1=0,
∴BC1⊥AC,BC1⊥AB1 ,
∵AC∩AB1=A,∴BC1⊥平面AB1C.
解:(Ⅱ)∵BC1⊥平面AB1C,∴ ![]() =(0,﹣1,1)是平面AB1C的法向量,
=(0,﹣1,1)是平面AB1C的法向量,
E(0, ![]() ,0),
,0), ![]() =(﹣1,0,
=(﹣1,0, ![]() ),
),
设平面AB1E的法向量 ![]() =(x,y,z),
=(x,y,z),
则 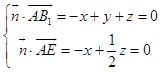 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,2),
=(1,﹣1,2),
设二面角E﹣AB1﹣C的大小为θ,
则cosθ= 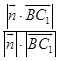 =
= ![]() =
= ![]() ,
,
∴θ=30°.
∴二面角E﹣AB1﹣C的大小为30°.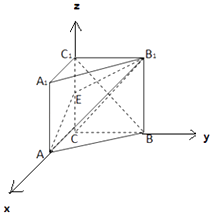
【解析】(Ⅰ)推导出AC⊥BC,以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能证明BC1⊥平面AB1C.(Ⅱ)求出平面AB1C的法向量,和平面AB1E的法向量,利用向量法能求出二面角E﹣AB1﹣C的大小.
【考点精析】利用直线与平面垂直的判定对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】在直角△ABC中,∠BCA=90°,CA=CB=1,P为AB边上的点且 ![]() =λ
=λ ![]() ,若
,若 ![]()
![]() ≥
≥ ![]()
![]() ,则λ的取值范围是( )
,则λ的取值范围是( )
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论: ①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为(注:把你认为正确的结论的序号都填上).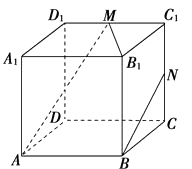
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图. 
(1)求a,并从频率分布直方图中求出成绩的众数和中位数;
(2)若老师从60分以下的人中选两个出来与之聊天,则这两人一个在(40,50]这一段,另一个在(50,60]这一段的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述: ①函数 ![]() 是奇函数;
是奇函数;
②函数 ![]() 的一条对称轴方程为
的一条对称轴方程为 ![]() ;
;
③函数 ![]() ,
, ![]() ,则f(x)的值域为
,则f(x)的值域为 ![]() ;
;
④函数 ![]() 有最小值,无最大值.
有最小值,无最大值.
所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题
(1)已知α为第二象限角,且 sinα= ![]() ,求
,求 ![]() 的值.
的值.
(2)已知α∈(0, ![]() ),β∈(0,π),且tan(α﹣β)=
),β∈(0,π),且tan(α﹣β)= ![]() ,tanβ=﹣
,tanβ=﹣ ![]() ,求tan(2α﹣β)的值及角2α﹣β.
,求tan(2α﹣β)的值及角2α﹣β.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有教职员工150人,其中高级职称15人,中级职称45人,一般职员90人,现在用分层抽样抽取30人,则样本中各职称人数分别为( )
A.5,10,15
B.3,9,18
C.3,10,17
D.5,9,16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com