
分析 斜边的平方等于两个直角边的平方和,可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和,边对应着面.
解答 解:由边对应着面,边长对应着面积,由类比可得:在四面体P-ABC中,平面PAB、平面PBC、平面PCA两两垂直,则△ABC面积的平方等于三个直角三角形面积的平方和.即$S_{△ABC}^2=S_{△PAB}^2+S_{△PBC}^2+S_{△PCA}^2$.
故答案为:在四面体P-ABC中,平面PAB、平面PBC、平面PCA两两垂直,则△ABC面积的平方等于三个直角三角形面积的平方和.即$S_{△ABC}^2=S_{△PAB}^2+S_{△PBC}^2+S_{△PCA}^2$.
点评 本题考查了从平面类比到空间,属于基本类比推理.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学/分 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理/分 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学/分 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理/分 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 17 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
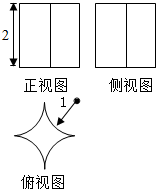 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  圆形区域 | |
| B. |  等腰三角形两腰与半椭圆围成的区域 | |
| C. | 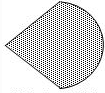 等腰三角形两腰与半圆围成的区域 | |
| D. | 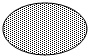 椭圆形区域 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com