
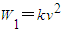 ,将v=10时W1=96代入即可算出k的值;
,将v=10时W1=96代入即可算出k的值;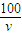 小时,可燃料费为96v,其余航行运作费用为
小时,可燃料费为96v,其余航行运作费用为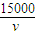 元,由此可得航行100海里的总费用为
元,由此可得航行100海里的总费用为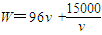 ,再运用基本不等式即可算出当且仅当v=12.5时,总费用W的最小值为2400(元).
,再运用基本不等式即可算出当且仅当v=12.5时,总费用W的最小值为2400(元).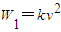 ,
,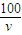 小时,可得其余航行运作费用为
小时,可得其余航行运作费用为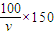 =
= 元
元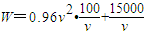 =
=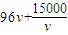 (0<v≤15)
(0<v≤15)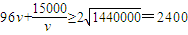 ,
,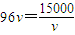 时,即
时,即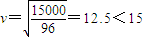 时,
时,

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:松江区二模 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013年上海市徐汇、松江、金山区高考数学二模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com