
【题目】若函数f(x)=lnx+ax2﹣(a+2)x在 ![]() 处取得极大值,则正数a的取值范围是
处取得极大值,则正数a的取值范围是
【答案】(0,2)
【解析】解:f(x)的定义域是(0,+∞),
f′(x)= ![]() +2ax﹣(a+2)=
+2ax﹣(a+2)= ![]() ,
,
①a≤0时,ax﹣1<0,
令f′(x)>0,解得:x> ![]() ,令f′(x)<0,解得:0<x<
,令f′(x)<0,解得:0<x< ![]() ,
,
故 ![]() 是函数的极小值点,不合题意,
是函数的极小值点,不合题意,
②0<a<2时, ![]() <
< ![]() ,
,
令f′(x)>0,解得:x< ![]() 或x>
或x> ![]() ,
,
令f′(x)<0,解得: ![]() <x<
<x< ![]() ,
,
∴f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴函数f(x)在 ![]() 处取得极大值,符合题意,
处取得极大值,符合题意,
③a=2时,f′(x)≥0,f(x)递增,无极值,
④a>2时, ![]() >
> ![]() ,
,
令f′(x)>0,解得:x> ![]() 或x<
或x< ![]() ,
,
令f′(x)<0,解得: ![]() <x<
<x< ![]() ,
,
∴f(x)在(0, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴函数f(x)在x= ![]() 处取得极大值,不符合题意,
处取得极大值,不符合题意,
综上,a∈(0,2),
所以答案是:(0,2).
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )
①当![]() 时,函数
时,函数![]() 在
在![]() 上是单调增函数;
上是单调增函数;
②当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;
上有最小值;
③函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
④方程![]() 可能有三个实数根.
可能有三个实数根.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知关于![]() 的一次函数
的一次函数![]()
(1)设集合![]() 和
和![]() 分别从集合
分别从集合![]() 和
和![]() 中随机取一个数作为
中随机取一个数作为![]() 和
和![]() ,求函数
,求函数![]() 是增函数的概率;
是增函数的概率;
(2)实数![]() 满足条件
满足条件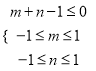 求函数
求函数![]() 的图象经过一、二、三象限的概率.
的图象经过一、二、三象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,河的两岸,分别有生活小区ABC和DEF,其中AB⊥BC,EF⊥DF,DF⊥AB,C,E,F三点共线,FD与BA的延长线交于点O,测得AB=3km,BC=4km,DF= ![]() km,FE=3km,EC=
km,FE=3km,EC= ![]() km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y=
km.若以OA,OD所在直线为x,y轴建立平面直角坐标系xoy,则河岸DE可看成是曲线y= ![]() (其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分.
(其中a,b为常数)的一部分,河岸AC可看成是直线y=kx+m(其中k,m为常数)的一部分. 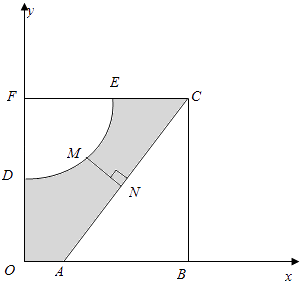
(1)求a,b,k,m的值;
(2)现准备建一座桥MN,其中M,N分别在DE,AC上,且MN⊥AC,设点M的横坐标为t.
①请写出桥MN的长l关于t的函数关系式l=f(t),并注明定义域;
②当t为何值时,l取得最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市若规划一居民小区ABCD,AD=2千米,AB=1千米,∠A=90°,政府决定从该地块中划出一个直角三角形地块AEF建活动休闲区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为1千米,△AEF的面积为S. 
(1)①设AE=x,求S关于x的函数关系式;
②设∠AEF=θ,求S关于θ的函数关系式;
(2)试确定点E的位置,使得直角三角形地块AEF的面积S最大,并求出S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x)﹣ln(1﹣x),则f(x)是( )
A.奇函数,且在(0,1)上是增函数
B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数
D.偶函数,且在(0,1)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们称满足下面条件的函数y=f(x)为“ξ函数”:存在一条与函数y=f(x)的图象有两个不同交点(设为P(x1 , y1)Q(x2 , y2))的直线,y=(x)在x= ![]() 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数:
①y= ![]() ②y=x2(x>0)③y=
②y=x2(x>0)③y= ![]() ④y=lnx,
④y=lnx,
其中为“ξ函数”的是(将所有你认为正确的序号填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com