练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知随机变量X～N(1,4)且P(X<2)＝0.72，则P(1<X<2)等于(　　)．
    A．0.36 B．0.16 C．0.22D．0.28
    C
    由P(X<2)＝0.72可得P(X≥2)＝1－0.72＝0.28，由正态曲线对称性可知P(X>1)＝0.5，所以P(1<X<2)＝P(X>1)－P(X≥2)＝0.5－0.28＝0.22.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

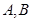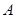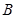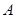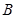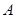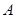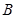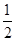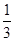    某中学为丰富教工生活，国庆节举办教工趣味投篮比赛，有两个定点投篮位置，在点投中一球得2分，在点投中一球得3分。某规则是：按先后再的顺序投篮，教师甲在和点投中的概率分别是和，且在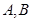两点投中与否相互独立。
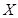    （1）若教师甲投篮三次，试求他投篮得分的分布列和数学期望；
    （2）若教师乙与教师甲在投中的概率相同，两人按规则各投三次，求甲胜乙的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    连掷两次骰子得到的点数分别为m和n，若记向量a＝(m，n)与向量b＝(1，－2)的夹角为θ，则θ为锐角的概率是________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    形状如图所示的三个游戏盘中(图①是正方形，M，N分别是所在边中点，图②是半径分别为2和4的两个同心圆，O为圆心，图③是正六边形，点P为其中心)各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．

    (1)一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？
    (2)用随机变量X表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量X的分布列．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    一个盒子里装有7张卡片，其中有红色卡片4张，编号分别为1,2,3,4；白色卡片3张，编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同)．
    (1)求取出的4张卡片中，含有编号为3的卡片的概率；
    (2)在取出的4张卡片中，红色卡片编号的最大值设为X，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    现有甲、乙两个靶．某射手向甲靶射击两次，每次命中的概率为，每命中一次得1分，没有命中得0分；向乙靶射击一次，命中的概率为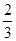，命中得2分，没有命中得0分，该射手每次射击的结果相互独立．假设该射手完成以上三次射击．
    (1)求该射手恰好命中两次的概率；
    (2)求该射手的总得分X的分布列及数学期望E(X)；
    (3)求该射手向甲靶射击比向乙靶射击多击中一次的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    将一枚均匀的硬币抛掷6次，则正面出现的次数比反面出现的次数多的概率为________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    先后抛掷2枚均匀的一分、二分的硬币，观察落地后硬币的正、反面情况，则下列事件包含3个基本事件的是 (　　)
    A．“至少一枚硬币正面向上”；
    B．“只有一枚硬币正面向上”；
    C．“两枚硬币都是正面向上”；
    D．“两枚硬币一枚正面向上，另一枚反面向上”.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某射手每次射击击中目标的概率均为，且每次射击的结果互不影响
    （I）假设这名射手射击3次，求至少2次击中目标的概率
    （II）假设这名射手射击3次，每次击中目标10分，未击中目标得0分，在3次射击中，若有两次连续击中目标，而另外一次未击中目标，则额外加5分；若3次全部击中，则额外加10分。用随机变量§表示射手射击3次后的总得分，求§的分布列和数学期望。

    查看答案和解析>>

    同步练习册答案