
【题目】在平面直角坐标系中,已知![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 且
且![]() .设
.设![]() .
.
(![]() )若
)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在区间
在区间![]() 内的解集.
内的解集.
(![]() )若函数
)若函数![]() 满足:图象关于点
满足:图象关于点![]() 对称,在
对称,在![]() 处取得最小值,试确定
处取得最小值,试确定![]() 、
、![]() 和
和![]() 应满足的与之等价的条件.
应满足的与之等价的条件.
【答案】(1)解集为![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(![]() )由平面向量数量积公式、结合辅助角公式可得
)由平面向量数量积公式、结合辅助角公式可得![]() ,令
,令![]() ,从而可得结果;(
,从而可得结果;(![]() )“图象关于点
)“图象关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”.因此,根据三角函数的图象特征可以知道,
取得最小值”.因此,根据三角函数的图象特征可以知道,![]() ,故有
,故有![]() ,
,
∴![]() ,
,![]() ,当且仅当
,当且仅当![]() ,
,![]() 时,
时,![]() 的图象关于点
的图象关于点![]() 对称;此时
对称;此时![]() ,
,![]() ,对
,对![]() 讨论两种情况可得使得函数
讨论两种情况可得使得函数![]() 满足“图象关于点
满足“图象关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值的充要条件”是“
取得最小值的充要条件”是“![]() ,
,![]() 时,
时,![]() ,
,![]() ;或当
;或当![]() 时,
时,![]() ,
,![]() ”.
”.
详解:(![]() )根据题意
)根据题意![]() ,
,
当![]() ,
,![]() ,
,![]() 时,
时,
![]() ,
,![]() ,
,
则有![]() 或
或![]() ,
,![]() .
.
即![]() 或
或![]() ,
,![]() .
.
又因为![]() ,故
,故![]() 在
在![]() 内的解集为
内的解集为![]() .
.
(![]() )解:因为
)解:因为![]() ,设周期
,设周期![]() .
.
因为函数![]() 须满足“图象关于点
须满足“图象关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”.
取得最小值”.
因此,根据三角函数的图象特征可以知道,![]() ,
,
故有![]() ,
,
∴![]() ,
,![]() ,
,
又因为,形如![]() 的函数的图象的对称中心都是
的函数的图象的对称中心都是![]() 的零点,
的零点,
故需满足![]() ,而当
,而当![]() ,
,![]() 时,
时,
因为![]() ,
,![]() ;
;
所以当且仅当![]() ,
,![]() 时,
时,
![]() 的图象关于点
的图象关于点![]() 对称;
对称;
此时,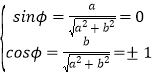 ,
,
∴![]() ,
,![]() .
.
(i)当![]() ,
,![]() 时,
时,![]() ,进一步要使
,进一步要使![]() 处
处![]() 取得最小值,
取得最小值,
则有![]() ,
,
∴![]() ,故
,故![]() ,
,![]() .
.
又![]() ,则有
,则有![]() ,
,![]() ,
,
因此,由![]() 可得
可得![]() ,
,![]() .
.
(ii)当![]() 时,
时,![]() ,进一步要使
,进一步要使![]() 处
处![]() 取得最小值,
取得最小值,
则有![]() ;
;
又![]() ,则有
,则有![]() ,
,![]() .
.
因此,由![]() ,可得
,可得![]() ,
,![]() .
.
综上,使得函数![]() 满足“图象关于点
满足“图象关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值的充要条件”是“
取得最小值的充要条件”是“![]() ,
,![]() 时,
时,![]() ,
,![]() ;或当
;或当![]() 时,
时,![]() ,
,![]() ”.
”.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某水产养殖基地要将一批海鲜用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由水产养殖基地承担.若水产养殖基地恰能在约定日期(×月×日)将海鲜送达,则销售商一次性支付给水产养殖基地![]() 万元;若在约定日期前送到,每提前一天销售商将多支付给水产养殖基地
万元;若在约定日期前送到,每提前一天销售商将多支付给水产养殖基地![]() 万元;若在约定日期后送到,每迟到一天销售商将少支付给水产养殖基地
万元;若在约定日期后送到,每迟到一天销售商将少支付给水产养殖基地![]() 万元.为保证海鲜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送海鲜,已知下表内的信息:
万元.为保证海鲜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送海鲜,已知下表内的信息:
汽车 行驶路线 | 不堵车的情况下到达城市乙所需时间(天) | 堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
公路 |
|
|
|
|
公路 |
|
|
|
|
(注:毛利润![]() 销售商支付给水产养殖基地的费用
销售商支付给水产养殖基地的费用![]() 运费)
运费)
(Ⅰ)记汽车走公路![]() 时水产养殖基地获得的毛利润为
时水产养殖基地获得的毛利润为![]() (单位:万元),求
(单位:万元),求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(Ⅱ)假设你是水产养殖基地的决策者,你选择哪条公路运送海鲜有可能让水产养殖基地获得的毛利润更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
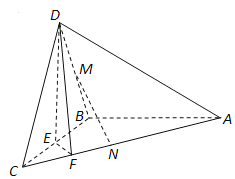
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 是正三角形,
是正三角形, ![]() 平面
平面![]() 为
为![]() 的中点,
的中点, ![]() 在棱
在棱![]() 上,且
上,且![]() .
.
(1)求三棱锥![]() 的体积;
的体积;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若![]() 为
为![]() 中点,
中点, ![]() 在棱
在棱![]() 上,且
上,且![]() ,求证:
,求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 为偶函数,对于函数
为偶函数,对于函数![]() 有下列几种描述:
有下列几种描述:
①![]() 是周期函数; ②
是周期函数; ②![]() 是它的一条对称轴;
是它的一条对称轴;
③![]() 是它图象的一个对称中心; ④当
是它图象的一个对称中心; ④当![]() 时,它一定取最大值;
时,它一定取最大值;
其中描述正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数,![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时,
时,![]() .
.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )若
)若![]() 在
在![]() 上为增函数,求
上为增函数,求![]() 的取值范围.
的取值范围.
(![]() )是否存在正整数
)是否存在正整数![]() ,使
,使![]() 的图象的最高点落在直线
的图象的最高点落在直线![]() 上?若存在,求出
上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2![]() cos
cos![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(1)求圆心的极坐标;
(2)求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足
满足![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() .
.
(1)若数列![]() 是首项为正数,公比为
是首项为正数,公比为![]() 的等比数列.
的等比数列.
①求证:数列![]() 为等比数列;
为等比数列;
②若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)已知![]() 为递增数列,即
为递增数列,即![]() .若对任意
.若对任意![]() ,数列
,数列![]() 中都存在一项
中都存在一项![]() 使得
使得![]() ,求证:数列
,求证:数列![]() 为等差数列.
为等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com