
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,当
,当![]() 时,若对任意
时,若对任意![]() ,存在
,存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() 和
和![]() ,
,
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ;
;
(2)![]() 的取值范围为
的取值范围为![]() .
.
【解析】试题分析:(1)首先求得函数![]() 的定义域与导函数,然后分
的定义域与导函数,然后分![]() 、
、![]() 、
、![]() 求得函数的单调区间;(2)首先结合(1)求得当
求得函数的单调区间;(2)首先结合(1)求得当![]() 时
时![]() 的最小值,然后利用分离参数法得
的最小值,然后利用分离参数法得![]() ,由此令
,由此令![]() ,从而根据
,从而根据![]() 的单调性求得其最小值,进而求得
的单调性求得其最小值,进而求得![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
, ![]()
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ,
,
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ,
,
由![]() 和
和![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() 和
和![]() .
.
当![]() 时,
时, ![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,
综上所述当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() 和
和![]() ,
,
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .
.
(2)当![]() 时,由(1)知
时,由(1)知![]() 在
在![]() ,
, ![]() ,依题意有
,依题意有![]() ,
,
∵![]()
![]()
![]() 在
在![]() 上有解,
上有解,
令![]() ,知
,知![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
∴![]()
∴![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .
.
或用![]() ,而
,而![]() ,对
,对![]() 分三种情况:
分三种情况:
①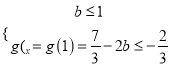
![]() 无解;
无解;
②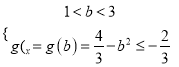
![]()
![]() ;
;
③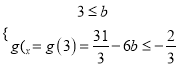
![]()
![]() .
.
综上:∴![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆的方程为x2+y2–2x+6y+8=0,那么通过圆心的一条直线方程是
A. 2x–y–1=0 B. 2x–y+1=0
C. 2x+y+1=0 D. 2x+y–1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某桔子园有平地和山地共120亩,现在要估计平均亩产量,按一定的比例用分层抽样的方法共抽取10亩进行调查.如果所抽山地是平地的2倍多1亩,则这个桔子园的平地与山地的亩数分别为________、________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)某小组有三名男生和两名女生,从中任选两名去参加比赛,则下列各对事件中为互斥事件的是( )
A.恰有一名男生和全是男生B.至少有一名男生和至少有一名女生
C.至少有一名男生和全是男生D.至少有一名男生和全是女生
查看答案和解析>>
科目:高中数学 来源: 题型:
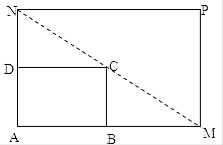
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米
(1)设AN的长为x米,用x表示矩形AMPN的面积?
(2)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取![]() 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位:![]() ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:
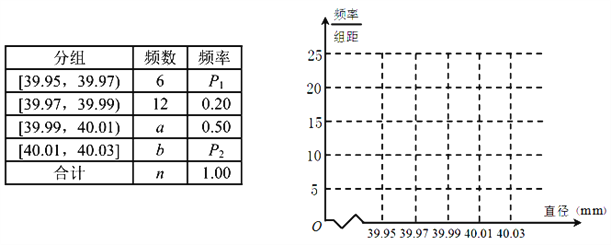
(1)求![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为![]() ,且称直径在
,且称直径在![]() 内的乒乓球为五星乒乓球,若这批乒乓球共有
内的乒乓球为五星乒乓球,若这批乒乓球共有![]() 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表,试估计这批乒乓球直径的平均值和中位数.
)作为代表,试估计这批乒乓球直径的平均值和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com