
【题目】(本小题满分16分)
在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,直线
,直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,且交椭圆
,且交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,连结
,连结![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,设直线
,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试探索当
,试探索当![]() 变化时,是否存在一条定直线
变化时,是否存在一条定直线![]() ,使得点
,使得点![]() 恒在直线
恒在直线![]() 上?若存在,请求出直线
上?若存在,请求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() (2)点
(2)点![]() 恒在直线
恒在直线![]() 上
上
【解析】试题分析:(1)直线![]() 与x轴的交点为椭圆
与x轴的交点为椭圆![]() 的右焦点
的右焦点![]() ,所以
,所以![]() 由
由![]() 得
得![]() 从而
从而![]() ,所以椭圆
,所以椭圆![]() 的标准方程为
的标准方程为![]() .(2)探索性问题,先通过特殊情形探索目标:令
.(2)探索性问题,先通过特殊情形探索目标:令![]() ,则根据对称性知满足题意的定直线
,则根据对称性知满足题意的定直线![]() 只能是
只能是![]() .问题转化为证明P,B,D三点共线,可利用斜率相等进行证明:设
.问题转化为证明P,B,D三点共线,可利用斜率相等进行证明:设![]() ,
, ![]() ,则
,则![]() ,从而
,从而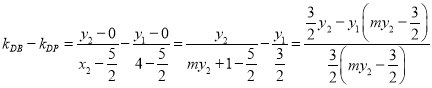
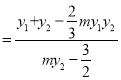 ,再利用直线与椭圆方程联立方程组得关于y的一元二次方程,由韦达定理得
,再利用直线与椭圆方程联立方程组得关于y的一元二次方程,由韦达定理得![]() 与
与![]() 关系,进而得
关系,进而得![]()
试题解析:(1)由题设,得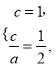 解得
解得![]() 从而
从而![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() . 4分
. 4分
(2)令![]() ,则
,则![]() ,
, ![]() 或者
或者![]() ,
, ![]() .
.
当![]() ,
, ![]() 时,
时, ![]() ;当
;当![]() ,
, ![]() 时,
时, ![]() ,
,
所以,满足题意的定直线![]() 只能是
只能是![]() . 6分
. 6分
下面证明点![]() 恒在直线
恒在直线![]() 上.
上.
设![]() ,
, ![]() ,由于
,由于![]() 垂直于
垂直于![]() 轴,所以点
轴,所以点![]() 的纵坐标为
的纵坐标为![]() ,从而只要证明
,从而只要证明![]() 在直线
在直线![]() 上. 8分
上. 8分
由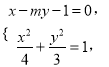 得
得![]() ,
,
![]() ,
,
![]() ,
, ![]() .① 10分
.① 10分
∵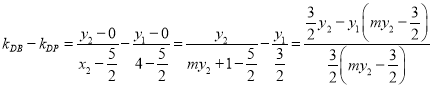
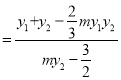 , 13分
, 13分
①式代入上式,得![]() , 所以
, 所以![]() . 15分
. 15分
∴点![]() 恒在直线
恒在直线![]() 上,从而直线
上,从而直线![]() 、直线
、直线![]() 与直线
与直线![]() 三线恒过同一点
三线恒过同一点
![]() , 所以存在一条定直线
, 所以存在一条定直线![]() :
: ![]() 使得点
使得点![]() 恒在直线
恒在直线![]() 上. 16分
上. 16分


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数g(x)满足g(x)=g′(1)ex﹣1﹣g(0)x+ ![]() ,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
A.(﹣∞,2]
B.(﹣∞,3]
C.[1,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4x﹣cos4x的最小正周期是π;
② ![]() =tanα;
=tanα;
③函数y=sinx+cosx的图象均关于点( ![]() ,0)成中心对称;
,0)成中心对称;
④把函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位得到y=3sin2x的图象.
个单位得到y=3sin2x的图象.
其中正确命题的编号是 . (写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知![]() 为实数,函数
为实数,函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,令
时,令![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若将其图象向右平移
)的最小正周期是π,若将其图象向右平移 ![]() 个单位后得到的图象关于原点对称,则函数f(x)的图象( )
个单位后得到的图象关于原点对称,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a、b、c是常数,则“a>0且b2﹣4ac<0”是“对任意x∈R,有ax2+bx+c>0”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a2+b2﹣c2= ![]() ab.
ab. 
(1)求角C的大小;
(2)如果0<A≤ ![]() ,m=2cos2
,m=2cos2 ![]() ﹣sinB﹣1,求实数m的取值范围.
﹣sinB﹣1,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,sinx),
=(sinx,sinx), ![]() =(﹣1,0)
=(﹣1,0)![]()
(1)若x= ![]() ,求
,求 ![]() 与
与 ![]() 的夹角θ;
的夹角θ;
(2)若x∈[﹣ ![]() ,
, ![]() ],f(x)=λ
],f(x)=λ ![]()
![]() 的最大值为
的最大值为 ![]() ,求λ.
,求λ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com