
分析 由x∈[0,$\frac{π}{4}$],利用单调性求得f(x)的范围,进一步求得g(x)的范围,依题意,对任意x1∈[0,$\frac{π}{4}$],存在x2∈[0,$\frac{π}{4}$],使得g(x1)=f(x2)成立,可得到关于m的不等式组,求解可求得实数m的取值范围.
解答 解:∵f(x)=sinx+cosx+sinxcosx=$\sqrt{2}sin(x+\frac{π}{4})+\frac{1}{2}sin2x$,
当x∈[0,$\frac{π}{4}$]时,函数f(x)为增函数,
∴f(x)min=f(0)=1,$f(x)_{max}=f(\frac{π}{4})=\sqrt{2}+\frac{1}{2}$,
∴f(x)∈[1,$\sqrt{2}+\frac{1}{2}$],
对于g(x)=mcos(2x-$\frac{π}{6}$)-2m+3(m>0),
2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{π}{3}$],mcos(2x-$\frac{π}{6}$)∈[$\frac{m}{2}$,m],
∴g(x)∈[-$\frac{3m}{2}$+3,3-m],
若对任意x1∈[0,$\frac{π}{4}$],存在x2∈[0,$\frac{π}{4}$],使得g(x1)=f(x2)成立,
则$\left\{\begin{array}{l}{1≤-\frac{3m}{2}+3}\\{\sqrt{2}+\frac{1}{2}≥3-m}\end{array}\right.$,
解得实数m的取值范围是[$\frac{5}{2}-\sqrt{2},\frac{4}{3}$].
故答案为:[$\frac{5}{2}-\sqrt{2},\frac{4}{3}$].
点评 本题考查两角和与差的正弦函数,着重考查三角函数的性质的运用,考查二倍角的余弦,解决问题的关键是理解对任意x1∈[0,$\frac{π}{4}$],存在x2∈[0,$\frac{π}{4}$],使得g(x1)=f(x2)成立的含义,是中档题.


科目:高中数学 来源: 题型:解答题
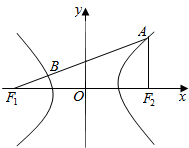 已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.
已知双曲线中心在原点,焦点在x轴上,过左焦点F1作倾斜角为30°的直线l,交双曲线于A,B两点,F2为双曲线的右焦点,且AF2⊥x轴,如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com