
(本题16分)
已知函数f(x)=x3-ax2-bx+a2,x∈R ,a,b为常数。
(1)若函数f(x)在x=1处有极值10,求实数a,b的值;
(2)若函数f(x)是奇函数,
①方程f(x)=2在x∈[-2,4]上恰有3个不相等的实数解,求实数b的取值范围;
②不等式f(x)+2b≥0对![]() x∈[1,4]恒成立,求实数b的取值范围。
x∈[1,4]恒成立,求实数b的取值范围。
(1)f’(x)=3x2-2ax-b,
由f(x)在x=1处有极值10,得f’(1)=0,f(1)=10。 …………2分
即3-2a-b=0,1-a-b+a‑2=10,解得a=3,b=-3或a=-4,b=11。 ……3分
经检验,a=3,b=-3不合题意,舍去。
∴a=-4,b=11。 ……………………………………4分
(2)由于函数f(x)的定义域为R,由函数f(x)是奇函数,得f(0)=0,∴a=0。 ……5分
①由f(x)=2,得f(x)-2=0,令g(x)=f(x)-2=x3-bx-2,则方程g(x)=0在x∈[-2,4]上恰有3个不相等的实数解。 ∵g’(x)=3x2-b,
(ⅰ)若b≤0,则g’(x)≥0恒成立,且函数g(x)不为常函数,∴g(x)在区间[-2,4]上为增函数,g(0)=0,所以,g(x)=0在区间[-2,4]上有且只有一个实数解。不合题意,舍去。
……………………………………6分
(ⅱ)若b>0,则函数g(x)在区间(-∞,-)上为增函数,在区间(-,)上为减函数,在区间(,+∞)上为增函数,由方程g(x)=0在x∈[-2,4]上恰有3个不相等的实数解,可得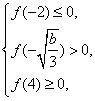 ……………………………………9分
……………………………………9分
解得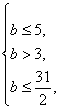 ∴b∈
∴b∈![]() ……………………………………10分
……………………………………10分
②由不等式f(x)+2b≥0,得x3-bx+2b≥0,即(x-2)b≤x3,
(ⅰ)若x-2=0即x=2时,b∈R; ……………………………………11分
(ⅱ)若x-2<0即x∈![]() 时,b≥在区间
时,b≥在区间![]() 上恒成立,令h(x)=,则b≥h(x)max。∵h’(x)=,∴h’(x)<0在x∈
上恒成立,令h(x)=,则b≥h(x)max。∵h’(x)=,∴h’(x)<0在x∈![]() 上恒成立,所以h(x)在区间
上恒成立,所以h(x)在区间![]() 上是减函数,∴h(x)max=h(1)=-1,∴b≥-1。 ……………………………………13分
上是减函数,∴h(x)max=h(1)=-1,∴b≥-1。 ……………………………………13分
(ⅲ)若x-2>0即x∈![]() 时,b≤在区间
时,b≤在区间![]() 上恒成立,则b≤h(x)min。由(ⅱ)可知,函数所以h(x)在区间
上恒成立,则b≤h(x)min。由(ⅱ)可知,函数所以h(x)在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数,∴h(x)min=h(3)=27,∴b≤27。 ……………………………………15分
上是增函数,∴h(x)min=h(3)=27,∴b≤27。 ……………………………………15分
综上所述,b∈[-1,27]。 ……………………………………16分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试理科数学 题型:解答题
((本题16分)
已知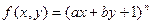 (常数
(常数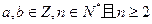 )
)
(1)若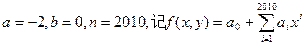 求:①
求:①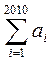 ;②
;②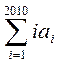
(2)若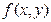 展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
查看答案和解析>>
科目:高中数学 来源:2014届江苏省无锡市高一下期中数学(艺术)试卷(解析版) 题型:解答题
(本题16分)已知函数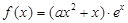 ,其中e是自然数的底数,
,其中e是自然数的底数,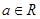 ,
,
(1)当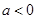 时,解不等式
时,解不等式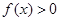 ;
;
(2)若当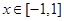 时,不等式
时,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)当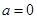 时,试判断:是否存在整数k,使得方程
时,试判断:是否存在整数k,使得方程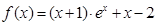 在
在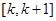
上有解?若存在,请写出所有可能的k的值;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三上学期期中考试理科数学试卷 题型:解答题
(本题16分)已知函数 在定义域
在定义域 上是奇函数,(其中
上是奇函数,(其中 且
且 ).
).
(1)求出 的值,并求出定义域
的值,并求出定义域 ;
;
(2)判断 在
在 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(3)当 时,
时, 的值域范围恰为
的值域范围恰为 ,求
,求 及
及 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011年江苏省如皋市五校高二下学期期中考试理科数学 题型:解答题
((本题16分)
已知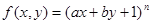 (常数
(常数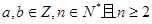 )
)
(1)若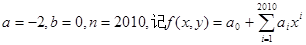 求:①
求:①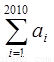 ;②
;②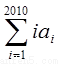
(2)若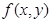 展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com