
【题目】已知过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() :
:![]() 交于点
交于点![]() 两点.
两点.
(1)求![]() 的取值范围;
的取值范围;
(2)请问是否存在实数k使得![]() (其中
(其中![]() 为坐标原点),如果存在请求出k的值,并求
为坐标原点),如果存在请求出k的值,并求![]() ;如果不存在,请说明理由。
;如果不存在,请说明理由。
【答案】(1)![]() (2)|MN|=2
(2)|MN|=2
【解析】
试题分析:(1)由题意可得,直线l的斜率存在,用点斜式求得直线l的方程,根据圆心到直线的距离等于半径求得k的值,可得满足条件的k的范围;(2)由题意可得,经过点M、N、A的直线方程为y=kx+1,根据直线和圆相交的弦长公式进行求解
试题解析:(1)由题意可得,直线l的斜率存在,
设过点A(0,1)的直线方程:y=kx+1,即:kx-y+1=0.
由已知可得圆C的圆心C的坐标(2,3),半径R=1.
故由![]() ,解得:
,解得:![]() .
.
故当![]() ,过点A(0,1)的直线与圆C:(x-2)2+(y-3)2=1相交于M,N两点.
,过点A(0,1)的直线与圆C:(x-2)2+(y-3)2=1相交于M,N两点.
(2)设M![]() ;N
;N![]() ,
,
由题意可得,经过点M、N、A的直线方程为y=kx+1,代入圆C的方程(x-2)2+(y-3)2=1,
可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() ,解得 k=1,
,解得 k=1,
故直线l的方程为 y=x+1,即 x-y+1=0.
圆心C在直线l上,MN长即为圆的直径.
所以|MN|=2


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中, CC1⊥平面ABC, AC⊥BC, AB1的中点为D,B1C∩BC1=E. 求证:
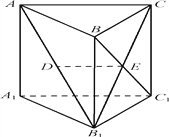
(1)DE∥平面AA1C1C;
(2)AC⊥平面BCC1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:![]() .
.
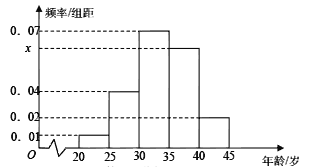
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
在四棱锥P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E为PA的中点.
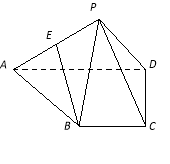
(1)求证:BE∥平面PCD;
(2)求证:平面PAB⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,![]() ,
,![]() .
.
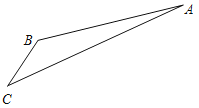
(Ⅰ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅱ)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=si n![]() -2cos2
-2cos2![]() +1.
+1.
(1)求f(x)的最小正周期;
(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当x∈![]() 时,y=g(x)的最大值.
时,y=g(x)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com