解:(1)当斜率不存在时,有
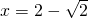
,圆心到直线的距离为

,符合题意;-----------(2分)
当斜率存在时,设切线方程为
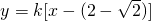
,
即
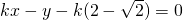
,
由圆心到切线的距离等于半径得:
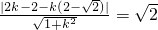
,
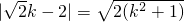
,---------------(4分)
得
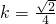
,所以
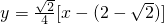
,
综上:所求切线方程为
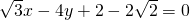
或
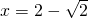
.-----(7分)
(2)由题意,⊙C关于x轴对称的圆C
1方程为(x-2)
2+(y+2)
2=2,----------(9分)
设过B与圆C
1相交且截得的弦长为2的直线l方程为y-3=k(x+3),
即kx-y+3+3k=0
由垂径定理得:
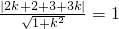
,----------(11分)
即
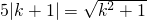
解得:
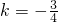
或
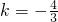
,---------(13分)
所以l方程为
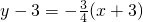
或
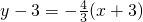
所以所求直线方程为3x+4y-3=0或4x+3y+3=0.---------(14分)
分析:(1)首先点A在圆外,故引⊙C的切线共有两条.斜率不存在时,符合题意;斜率存在时,利用圆心到直线的距离等于半径,可求切线方程;
(2)根据对称性,将反射光线被⊙C所截得的弦长为2等价转化为入射光线被⊙C关于x轴对称圆所截得的弦长为2,从而可求入射光线l所在的直线方程.
点评:本题的考点是直线和圆的方程的应用,主要考查圆的切线方程,圆的对称性,关键是利用圆的特殊性,利用圆心到直线的距离解决直线和圆的位置关系问题.

 ,0)的⊙C的切线方程;
,0)的⊙C的切线方程;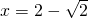 ,圆心到直线的距离为
,圆心到直线的距离为 ,符合题意;-----------(2分)
,符合题意;-----------(2分)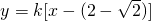 ,
,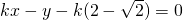 ,
,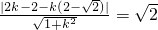 ,
,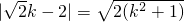 ,---------------(4分)
,---------------(4分)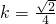 ,所以
,所以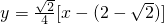 ,
,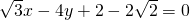 或
或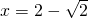 .-----(7分)
.-----(7分)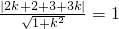 ,----------(11分)
,----------(11分)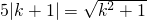
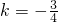 或
或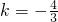 ,---------(13分)
,---------(13分)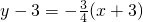 或
或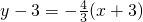


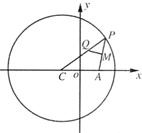 已知C为圆(x+
已知C为圆(x+ ,0)的⊙C的切线方程;
,0)的⊙C的切线方程;