
【题目】已知函数![]() .
.
(1)当x∈[1,4]时,求函数![]() 的值域;
的值域;
(2)如果对任意的x∈[1,4],不等式![]() 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
【答案】(1) [0,2]. (2) (-∞,-3).
【解析】试题分析:(1) 令t=log2x,则函数h(x)转化为关于t 的二次函数:h(x)=-2(t-1)2+2 ,根据x∈[1,4],得t∈[0,2],结合对称轴与定义区间位置关系确定函数最值和值域(2) 令t=log2x,则(3-4t)(3-t)>k·t对一切t∈[0,2]恒成立,当t=0时,k∈R;当t∈(0,2]时,利用变量分离法转化为对应函数最值:![]() 最小值,根据基本不等式求最值:
最小值,根据基本不等式求最值:![]() 即得实数k的取值范围
即得实数k的取值范围
试题解析:(1)h(x)=(4-2log2x)·log2x=-2(log2x-1)2+2,
因为x∈[1,4],所以log2x∈[0,2],
故函数h(x)的值域为[0,2].
(2)由f(x2)·f()>k·g(x),
得(3-4log2x)(3-log2x)>k·log2x,
令t=log2x,因为x∈[1,4],所以t=log2x∈[0,2],
所以(3-4t)(3-t)>k·t对一切t∈[0,2]恒成立,
①当t=0时,k∈R;
②当t∈(0,2]时,![]() 恒成立,即
恒成立,即![]() ,因为
,因为![]() ,当且仅当
,当且仅当![]() 即
即![]() 时取等号,所以
时取等号,所以![]() 的最小值为-3,
的最小值为-3,
综上,k∈(-∞,-3).


科目:高中数学 来源: 题型:
【题目】某运输队接到给灾区运送物资的任务,该运输队有8辆载重为![]() 的
的![]() 型卡车,6辆载重为
型卡车,6辆载重为![]() 的
的![]() 型卡车,10名驾驶员,要求此运输队每天至少运送
型卡车,10名驾驶员,要求此运输队每天至少运送![]() 救灾物资.已知每辆卡车每天往返的次数为
救灾物资.已知每辆卡车每天往返的次数为![]() 型卡车16次,
型卡车16次, ![]() 型卡车12次.每辆卡车每天往返的成本为
型卡车12次.每辆卡车每天往返的成本为![]() 型卡车240元,
型卡车240元, ![]() 型卡车378元.问每天派出
型卡车378元.问每天派出![]() 型卡车与
型卡车与![]() 型卡车各多少辆,运输队所花的成本最低?
型卡车各多少辆,运输队所花的成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列A:a1,a2,…,an(0≤a1<a2<…<an,n≥3)具有性质P:对任意i,j(1≤i≤j≤n),aj+ai与aj-ai两数中至少有一个是该数列中的一项。现给出以下四个结论:
①数列0,1,3具有性质P;
②数列0,2,4,6具有性质P;
③若数列A具有性质P,则a1=0;
④若数列a1,a2,a3(0≤a1<a2<a3)具有性质P,则a1+a3=2a2。
其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
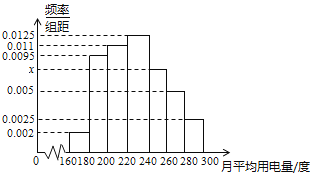
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
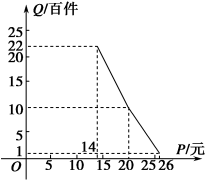
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,直线
,直线![]() ,过右焦点
,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 和
和![]() 于点
于点![]() .
.
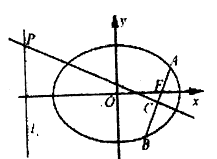
(1)求弦长![]() 的最小值;
的最小值;
(2)在直线![]() 上任取一点
上任取一点![]() ,当
,当![]() 的斜率
的斜率![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com