
【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
【答案】
(1)
解:(1)∵y2=2px过点P(1,1),
∴1=2p,
解得p= ![]() ,
,
∴y2=x,
∴焦点坐标为( ![]() ,0),准线为x=﹣
,0),准线为x=﹣ ![]() ,
,
(2)
(2)证明:设过点(0, ![]() )的直线方程为
)的直线方程为
y=kx+ ![]() ,M(x1,y1),N(x2,y2),
,M(x1,y1),N(x2,y2),
∴直线OP为y=x,直线ON为:y= ![]() x,
x,
由题意知A(x1,x1),B(x1, ![]() ),
),
由 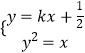 ,可得k2x2+(k﹣1)x+
,可得k2x2+(k﹣1)x+ ![]() =0,
=0,
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]()
∴y1+ ![]() =kx1+
=kx1+ ![]() +
+ ![]() =2kx1+
=2kx1+ ![]() =2kx1+
=2kx1+ 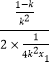 =
= ![]()
∴A为线段BM的中点.
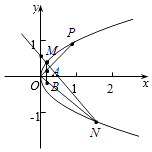
【解析】(1.)根据抛物线过点P(1,1).代值求出p,即可求出抛物线C的方程,焦点坐标和准线方程;
(2.)设过点(0, ![]() )的直线方程为y=kx+
)的直线方程为y=kx+ ![]() ,M(x1 , y1),N(x2 , y2),根据韦达定理得到x1+x2=
,M(x1 , y1),N(x2 , y2),根据韦达定理得到x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,根据中点的定义即可证明.
,根据中点的定义即可证明.


科目:高中数学 来源: 题型:
【题目】设a∈Z,已知定义在R上的函数f(x)=2x4+3x3﹣3x2﹣6x+a在区间(1,2)内有一个零点x0 , g(x)为f(x)的导函数.
(Ⅰ)求g(x)的单调区间;
(Ⅱ)设m∈[1,x0)∪(x0 , 2],函数h(x)=g(x)(m﹣x0)﹣f(m),求证:h(m)h(x0)<0;
(Ⅲ)求证:存在大于0的常数A,使得对于任意的正整数p,q,且 ![]() ∈[1,x0)∪(x0 , 2],满足|
∈[1,x0)∪(x0 , 2],满足| ![]() ﹣x0|≥
﹣x0|≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°.

(1)求证:EF⊥PB.
(2)试问:当点E在线段AB上移动时,二面角PFCB的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系.

(1)求平面A1B1C的法向量;
(2)求直线AC与平面A1B1C夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于概率和统计的几种说法:
①10名工人某天生产同一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则a,b,c的大小关系为c>a>b;
②样本4,2,1,0,-2的标准差是2;
③在面积为S的△ABC内任选一点P,则随机事件“△PBC的面积小于![]() ”的概率为
”的概率为![]() ;
;
④从写有0,1,2,…,9的十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片上的数字各不相同的概率是![]() .
.
其中正确说法的序号有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b为异面直线,且所成的角为70°,过空间一点作直线l,直线l与a,b均异面,且所成的角均为50°,则满足条件的直线共有( ) 条
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4 , 坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为 ![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为 ![]() (t为参数).(10分)
(t为参数).(10分)
(1)若a=﹣1,求C与l的交点坐标;
(2)若C上的点到l距离的最大值为 ![]() ,求a.
,求a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com