
【题目】已知圆![]() ,圆
,圆![]() ,经过原点的两直线
,经过原点的两直线![]() 满足
满足![]() ,且
,且![]() 交圆
交圆![]() 于不同两点交
于不同两点交![]() ,
, ![]() 圆
圆![]() 于不同两点
于不同两点![]() ,记
,记![]() 的斜率为
的斜率为![]()
(1)求![]() 的取值范围;
的取值范围;
(2)若四边形![]() 为梯形,求
为梯形,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】试题分析:(1)首先根据条件设出直线![]() 的方程,然后利用点到直线的距离公式求得
的方程,然后利用点到直线的距离公式求得![]() 的取值范围,;(2)首先设出点
的取值范围,;(2)首先设出点![]() 的坐标,然后分别将
的坐标,然后分别将![]() 的方程代入圆的方程,从而利用韦达定理,结合梯形的性质求得
的方程代入圆的方程,从而利用韦达定理,结合梯形的性质求得![]() 的值.
的值.
试题解析:(1)显然k≠0,所以l1:y=kx,l2:y=-x.
依题意得M到直线l1的距离d1=<,
整理得k2-4k+1<0,解得2-<k<2+; …2分
同理N到直线l2的距离d2=<,解得-<k<, …4分
所以2-<k<. …5分
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
将l1代入圆M可得(1+k2)x2-4(1+k)x+6=0,
所以x1+x2=,x1x2=; …7分
将l2代入圆N可得:(1+k2)x2+16kx+24k2=0,
所以x3+x4=-,x3x4=. …9分
由四边形ABCD为梯形可得,所以=,
所以(1+k)2=4,解得k=1或k=-3(舍). …12分


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1+sin2x,sinx﹣cosx),
=(1+sin2x,sinx﹣cosx), ![]() =(1,sinx+cosx),函数f(x)=
=(1,sinx+cosx),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大值及取得最大值相应的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多 ![]() ,则x+y的值为( )
,则x+y的值为( ) 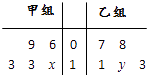
A.5
B.4
C.3
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生. 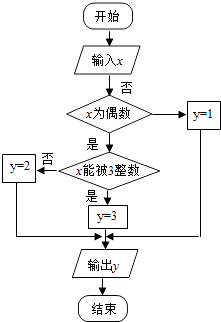
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.
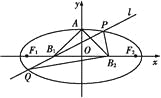
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com