
分析 (Ⅰ)根据平面向量数量积的坐标表示与三角恒等变换,化简f(x),求出它的增区间;
(Ⅱ)利用二倍角公式化简f(α),再根据同角的三角函数关系,即可求出f(α)的值.
解答 解:(Ⅰ)向量$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=(cos(x+$\frac{π}{6}$)+sinx,cosx),
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=sinxcos(x+$\frac{π}{6}$)+sin2x+cos2x
=sinxcosxcos$\frac{π}{6}$-sinxsinxsin$\frac{π}{6}$+1
=$\frac{\sqrt{3}}{2}$sinxcosx-$\frac{1}{2}$sin2x+1
=$\frac{\sqrt{3}}{4}$sin2x-$\frac{1}{2}$•$\frac{1-cos2x}{2}$+1
=$\frac{1}{2}$($\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x)+$\frac{3}{4}$
=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)+$\frac{3}{4}$,…4分
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,
解得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z,
故f(x)的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z;…6分
(Ⅱ)由f(α)=$\frac{1}{2}$sin(2α+$\frac{π}{6}$)+$\frac{3}{4}$=sin(α+$\frac{π}{12}$)cos(α+$\frac{π}{12}$)+$\frac{3}{4}$,…8分
又$cos(α+\frac{π}{12})=\frac{1}{3}$,且$α∈(0,\frac{π}{2})$,
∴sin(α+$\frac{π}{12}$)=$\sqrt{1{-(\frac{1}{3})}^{2}}$=$\frac{2\sqrt{2}}{3}$,…10分
∴f(α)=$\frac{1}{3}$×$\frac{2\sqrt{2}}{3}$+$\frac{3}{4}$=$\frac{2\sqrt{2}}{9}$+$\frac{3}{4}$.…12分
点评 本题考查了三角函数的化简与运算问题,也考查了平面向量的数量积运算问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | x-3y=0 | B. | 2x-y-5=0 | C. | x+y-4=0 | D. | x-2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p2 | B. | p2(1-p) | C. | ${C}_{3}^{2}$p2 | D. | ${C}_{3}^{2}$p2(1-p) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下:
2016年1月1日,我国实施“全面二孩”政策,中国社会科学院在某地随机抽取了150名已婚男性,其中愿意生育二孩的有100名,经统计,该100名男性的年龄情况对应的频率分布直方图如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.
如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
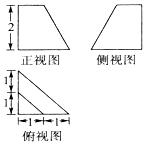
| A. | $\frac{7}{3}$ | B. | 7 | C. | 13 | D. | $\frac{{17+3\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com