
(本小题共12分)已知向量 ,
, ,函数
,函数 .
.
(Ⅰ)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(Ⅱ)求函数 在区间
在区间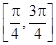 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)最小正周期是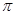 ;最大值是
;最大值是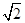 +1(Ⅱ)最大值是2,最小值是1
+1(Ⅱ)最大值是2,最小值是1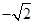
【解析】
试题分析:(Ⅰ)因为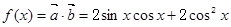 ,
…1分
,
…1分
所以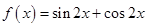 +1
…2分
+1
…2分
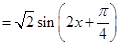 +1.
…3分
+1.
…3分
所以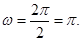 …4分
…4分
又因为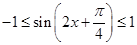 ,
,
所以1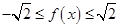 +1.
…5分
+1.
…5分
所以函数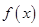 的最小正周期是
的最小正周期是 ;最大值是
;最大值是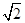 +1.
…6分
+1.
…6分
(Ⅱ)由(Ⅰ)知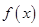
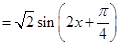 +1.
+1.
因为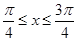 ,所以
,所以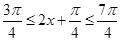 .
…7分
.
…7分
所以当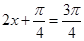 ,即
,即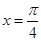 时,函数
时,函数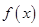 有最大值是2;
…9分
有最大值是2;
…9分
当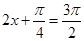 ,即
,即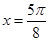 时,函数
时,函数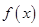 有最小值是1
有最小值是1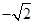 .
…11分
.
…11分
所以函数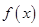 在区间
在区间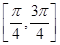 上的最大值是2,最小值是1
上的最大值是2,最小值是1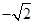 .
…12分
.
…12分
考点:本小题以向量为载体,考查三角函数的图象和性质,考查学生对三角函数公式的掌握和对三角函数图象的理解和应用.
点评:平面向量与三角的综合性问题大多是以三角题型为背景的一种向量描述.它需要根据向量运算性质将向量问题转化为三角的相关知识来解答,三角知识是考查的主体.考查的要求并不高,解题时要综合利用平面向量的几何意义等将题中的条件翻译成简单的数学问题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源:2013届甘肃省高三第二次检测理科数学试卷(解析版) 题型:解答题
(本小题共12分)
已知函数f(x)=2x- -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年内蒙古呼伦贝尔市高三第四次模拟考试文科数学试卷 题型:解答题
(本小题共12分)已知曲线 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(- ,0)和F2(
,0)和F2( ,0)的距离之和为4.
,0)的距离之和为4.
(1)求曲线 的方程;
的方程;
(2)设过(0,-2)的直线 与曲线
与曲线 交于C、D两点,且
交于C、D两点,且 为坐标原点),求直线
为坐标原点),求直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高一上学期期中考试数学试卷 题型:解答题
(本小题共12分)
已知函数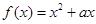 的最小值不小于
的最小值不小于 , 且
, 且 .
.
(1)求函数 的解析式;
的解析式;
(2)函数 在
在 的最小值为实数
的最小值为实数 的函数
的函数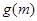 ,求函数
,求函数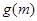 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com