练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇环形ABCD,作圆台容器的侧面,并且在余下的扇形OCD内能剪下一块与其相切的圆形使它恰好作圆台容器的下底面(大底面).试求:

    (1)AD应取多长?

    (2)容器的容积为多大?

    【答案】（1）36；（2）

    【解析】试题分析：（1）设圆台上、下底面半径分别为，则，由题意得 ，由此能求出 长．
    （2）圆台所在圆锥的高 ，圆台的高 ，由此能求出容器的容积．

    试题解析;(1)如图,设圆台上、下底面半径分别为r,R,AD=xcm,则OD=(72-x)cm.

    由题意得所以R=12,r=6,x=36,所以AD=36cm.

    (2)圆台所在圆锥的高H==12,圆台的高h==6,小圆锥的高h'=6,

    所以V容=V大锥-V小锥=πR2H-πr2h'=504π.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数的定义域为，对任意实数，都有.

    （1）若， ，且，求， 的值；

    （2）若为常数，函数是奇函数，

    ①验证函数满足题中的条件；

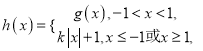    ②若函数求函数的零点个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，，，，，分别为的中点，.

    （1）求证：平面平面；

    （2）设，若平面与平面所成锐二面角，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一家医药研究所，从中草药中提取并合成了甲、乙两种抗“病毒”的药物，经试验，服用甲、乙两种药物痊愈的概率分别为.现已进入药物临床试用阶段，每个试用组由4位该病毒的感染者组成，其中2人试用甲种抗病毒药物，2人试用乙种抗病毒药物，如果试用组中，甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数，则称该组为“甲类组”.

    （1）求一个试用组为“甲类组”的概率；

    （2）观察3个试用组，用表示这3个试用组中“甲类组”的个数，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分15分）在直三棱柱中，底面是边长为2的正三角形， 是棱的中点，且.

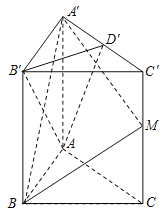
    （1）试在棱上确定一点，使平面；

    （2）当点在棱中点时，求直线与平面所成角的大小的正弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数 在 处取得极值．

    （1）求 的单调区间；

    （2）若 在定义域内有两个不同的零点，求实数 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个焦点与抛物线的焦点重合，且点到直线的距离为， 与的公共弦长为.

    （1）求椭圆的方程及点的坐标；

    （2）过点的直线与交于两点，与交于两点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如下表：

    年 份

    2008

    2009

    2010

    2011

    2012

    2013

    2014

    年份代号t

    1

    2

    3

    4

    5

    6

    7

    人均纯收入y

    2.7

    3.6

    3.3

    4.6

    5.4

    5.7

    6.2

    对变量t与y进行相关性检验，得知t与y之间具有线性相关关系．

    （1）求y关于t的线性回归方程；

    （2）预测该地区2017年的居民人均纯收入．

    附：回归直线的斜率和截距的最小二乘估计公式分别为：

    ，

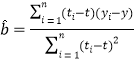    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.

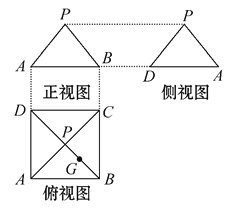
    (1)根据三视图,画出该几何体的直观图.

    (2)在直观图中,①证明:PD∥平面AGC;

    ②证明:平面PBD⊥平面AGC.

    查看答案和解析>>

    同步练习册答案