
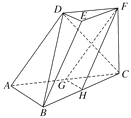
【题目】如图,三棱台DEF ABC中,AB=2DE,G,H分别为AC,BC的中点.
(1)求证:平面ABED∥平面FGH;
(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)根据面面平行的判定定理即可证明平面ABED∥平面GHF;连接HE,利用三角形中位线定理可得GH∥AB,于是GH⊥BC.可证明EFCH是平行四边形,可得HE⊥BC.因此BC⊥平面EGH,即可证明平面BCD⊥平面EGH.
解析:
(1)在三棱台DEFABC中,![]() BC=2EF,H为BC的中点,
BC=2EF,H为BC的中点,![]() BH∥EF,BH=EF,
BH∥EF,BH=EF,
![]() 四边形BHFE为平行四边形,有BE∥HF.
四边形BHFE为平行四边形,有BE∥HF.
![]() BE∥平面FGH
BE∥平面FGH
在△ABC中,![]() G为AC的中点,H为BC的中点,
G为AC的中点,H为BC的中点,![]() GH∥AB.
GH∥AB.
![]() AB∥平面FGH
AB∥平面FGH
又AB∩BE=B,所以平面ABED∥平面FGH.
(2)连接HE,EG
![]() G,H分别为AC,BC的中点,
G,H分别为AC,BC的中点,![]() GH∥AB.
GH∥AB. ![]() AB⊥BC,
AB⊥BC,![]() GH⊥BC.
GH⊥BC.
又![]() H为BC的中点,
H为BC的中点,![]() EF∥HC,EF=HC,
EF∥HC,EF=HC,![]() 四边形EFCH是平行四边形,有CF∥HE.
四边形EFCH是平行四边形,有CF∥HE.
![]() CF⊥BC,
CF⊥BC,![]() HE⊥BC.
HE⊥BC.
![]() HE,GH平面EGH,HE∩GH=H,
HE,GH平面EGH,HE∩GH=H,![]() BC⊥平面EGH.
BC⊥平面EGH.
![]() BC平面BCD,
BC平面BCD,![]() 平面BCD⊥平面EGH.
平面BCD⊥平面EGH.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现.某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:

用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若用户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.试应用样本估计总体的思想,估计该地区满意度等级为“
级”.试应用样本估计总体的思想,估计该地区满意度等级为“![]() 级”的用户所占的百分比是多少?(精确到
级”的用户所占的百分比是多少?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,BC边上的高所在的直线方程为x﹣2y+1=0,∠A的平分线所在直线的方程为y=0.
(1)求点A的坐标;
(2)若点B的坐标为(1,2),求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知动圆S过定点P(﹣2 ![]() ),且与定圆Q:(x﹣2
),且与定圆Q:(x﹣2 ![]() )2+y2=36相切,记动圆圆心S的轨迹为曲线C.
)2+y2=36相切,记动圆圆心S的轨迹为曲线C.
(1)求曲线C的方程;
(2)设曲线C与x轴,y轴的正半轴分别相交于A,B两点,点M,N为椭圆C上相异的两点,其中点M在第一象限,且直线AM与直线BN的斜率互为相反数,试判断直线MN的斜率是否为定值.如果是定值,求出这个值;如果不是定值,说明理由;
(3)在(2)条件下,求四边形AMBN面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣k ln x,k>0.
﹣k ln x,k>0.
(1)求f(x)的单调区间和极值;
(2)证明:若f(x)存在零点,则f(x)在区间(1, ![]() ]上仅有一个零点.
]上仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:Sn=1﹣an(n∈N*),其中Sn为数列{an}的前n项和. (Ⅰ)试求{an}的通项公式;
(Ⅱ)若数列{bn}满足: ![]() (n∈N*),试求{bn}的前n项和公式Tn .
(n∈N*),试求{bn}的前n项和公式Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com