
若函数 为奇函数,则a=
为奇函数,则a=
A.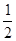 | B.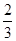 | C.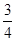 | D.1 |
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:单选题
某种商品,现在每件定价p元,每月卖n件。根据市场调查显示,定价每上涨x
成,卖出的数量将会减少y成,如果涨价后的销售总金额是现在的1.2倍,则用x来表示
y的函数关系式为( )
A.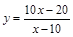 | B.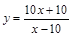 | C.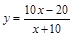 | D.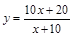 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com