
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,D,E分别为BC,PD的中点,F为AB上一点,且
,D,E分别为BC,PD的中点,F为AB上一点,且![]() .
.
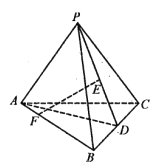
(1)求证:![]() 平面PAD;
平面PAD;
(2)求证:![]() 平面PAC;
平面PAC;
(3)若二面角![]() 为60°,求三棱锥
为60°,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)根据一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直,即证得;(2)根据平面外一条直线和此平面内的一条直线平行,那么这条直线和这个平面平行,在平面PAC中找一条直线与EF平行,即得证;(3)由二面角![]() 为60°,可知
为60°,可知![]() 的面积,再由三棱锥的体积公式即得。
的面积,再由三棱锥的体积公式即得。
解:(1)证明:因为![]() ,
,![]() ,D是BC的中点,
,D是BC的中点,
所以![]() ,
,![]() ,
,
所以,![]() 平面PAD.
平面PAD.
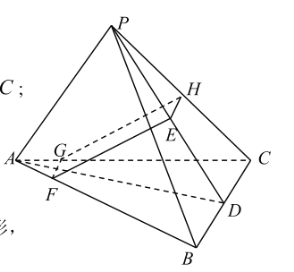
(2)证明:在AC上取一点G,使得![]() ,
,
取PC的中点H连接FG、GH、HE,
在![]() 中,有
中,有![]() ,
,![]() ,则
,则![]() ;
;
在![]() 中,E、H分别是PD、PC的中点,
中,E、H分别是PD、PC的中点,
则![]() ,
,![]() ;
;
所以,![]() ,所以,四边形EFGH为平行四边形,
,所以,四边形EFGH为平行四边形,
所以,![]() ,又
,又![]() 平面PAC,
平面PAC,![]() 平面PAC,
平面PAC,
所以,![]() 平面PAC.
平面PAC.
(3)由(1)知![]() ,
,![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,
,
所以,![]() ,
,
所以,三棱锥![]() 的体积
的体积![]() .
.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】在坐标平面上,纵横坐标都是整数的点称为整点.试证:存在一个同心圆的集合,使得:(1)每个整点都在此集体的某一圆周上;(2)此集合的每个圆周上.有且只有一个整点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(![]() )天的销售价格(单位:元/件)为
)天的销售价格(单位:元/件)为![]() ,第x天的销售量(单位:件)为
,第x天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
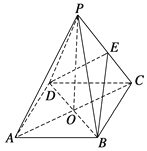
【题目】如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:平面PAC⊥平面BDE;
(2)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间,某旅行社为吸引游客去某风景区旅游,推出如下收费标准:若旅行团人数不超过30,则每位游客需交费用600元;若旅行团人数超过30,则游客每多1人,每人交费额减少10元,直到达到70人为止.
(1)写出旅行团每人需交费用![]() (单位:元)与旅行团人数
(单位:元)与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)旅行团人数为多少时,旅行社可以从该旅行团获得最大收入?最大收入是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足x3<y3,则下列不等式中恒成立的是( )
A. (![]() )x>(
)x>(![]() )y B. ln(x2+1)>ln(y2+1)
)y B. ln(x2+1)>ln(y2+1)
C. ![]() D. tanx>tany
D. tanx>tany
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且 .
.
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入﹣年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现对一块边长8米的正方形场地ABCD进行改造,点E为线段BC的中点,点F在线段CD或AD上(异于A,C),设![]() (米),
(米),![]() 的面积记为
的面积记为![]() (平方米),其余部分面积记为
(平方米),其余部分面积记为![]() (平方米).
(平方米).
(1)当![]() (米)时,求
(米)时,求![]() 的值;
的值;
(2)求函数![]() 的最大值;
的最大值;
(3)该场地中![]() 部分改造费用为
部分改造费用为![]() (万元),其余部分改造费用为
(万元),其余部分改造费用为![]() (万元),记总的改造费用为W(万元),求W取最小值时x的值.
(万元),记总的改造费用为W(万元),求W取最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com