练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题满分12分）
    5个人排成一排，按下列要求各有多少种不同的排法？
    （1）其中甲不站排头，乙不站排尾；
    （2）其中甲、乙2人必须相邻；
    （3）其中甲、乙2人不能相邻；
    （4）其中甲、乙中间有且只有1人；
    （5）其中甲只能站在乙的左侧．
    （1）（捆绑法）将甲、乙二人绑在一起作为一个元素与其他3个元素作全排列，共有种，甲、乙内部有种排法，故共有=48种．     3分
    （2）（插空法）先将甲、乙2人之外的3人排好，有种排法，这三人之间及两端形成四个空位，再将甲、乙插入到这4个空中去，有种排法，故共有=72种．
    3分
    （3）甲、乙二人有种排法，再从剩下的3人中选1人插入他们之间，有种方法，然后将这三人看作一个元素，和其他2个元素做全排列，有种，故共有=36种．
    （4）五个人的全排列为种，这些排列中甲、乙的不同顺序的排法有，但只有一种是符合要求的，故满足条件的排法有=60种
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    某电视台连续播放5个广告，其中有3个不同的商业广告和2个不同的公益广告，要求最后播放的不能是商业广告且两个公益广告不能连续播放，则不同的播放方式有　     种（用数字作答）．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

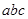    如果三位正整数如“”满足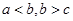，则这样的三位数称为凸数（如120,352）
    那么，所有的三位凸数的个数为                                 （   ）
    A．240B．204C．729D．920

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    用数字0，1，2，3，4，5，可以组成          个没有重复数字的6位偶数。（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    在二项式的展开式中，前三项系数的绝对值成等差数列．（12分）（１）求展开式的第四项；（２）求展开式的常数项；

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    ．将数字1，2，3，4，5按第一行2个数，第二行3个数的形式随机排列，设表示第i行中最小的数，则满足的所有排列的个数是       。（用数学作答）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某校开设A类选修课3门，B类选择课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有
    A．30种B．35种C．42种 D．48种

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    将3个不同的小球放入编号分别为1,2,3,4的盒子内,则4号盒子中至少有一个球的放法有_______种（用数字作答）.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在汶川地震的灾后重建工作中，国务院指示江西省有对口援助受灾相对较轻的小金县，现我省选派6名教师（其中4名男、2名女教师）到小金县的A、B、C三个乡镇中学支教，每个乡镇2名，且2名女教师不在同一乡镇，也不在C镇，某男教师甲不在A镇，问共有多少选派方法（   ）
    A．24             B．18             C．12              D．9

    查看答案和解析>>

    同步练习册答案