
某公司承担了每天至少搬运280吨水泥的任务,已知该公司有6辆A型卡车和8辆B型卡车.又已知A型卡车每天每辆的运载量为30吨,成本费为0.9千元;B型卡车每天每辆的运载量为40吨,成本费为1千元.
(1)如果你是公司的经理,为使公司所花的成本费最小,每天应派出A型卡车、B型卡车各多少辆?
(2)在(1)的所求区域内,求目标函数 的最大值和最小值.
的最大值和最小值.
(1) 型卡车0辆,
型卡车0辆,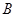 型卡车
型卡车 辆;(2)在
辆;(2)在 处取最大值
处取最大值 ,在
,在 处取最小值
处取最小值 .
.
解析试题分析:(1)根据题意可得出关于A型卡车、B型卡车的一组限制条件 ,由目标函数
,由目标函数 化简得
化简得 ,平移直线可得当直线经过点
,平移直线可得当直线经过点 时,直线在
时,直线在 轴上的截距最小,即
轴上的截距最小,即 取最小值,为
取最小值,为 ;(2)由目标函数
;(2)由目标函数 可联想到两点确定的斜率坐标公式
可联想到两点确定的斜率坐标公式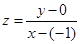 ,这是两点
,这是两点 之间的斜率,结合图象不难发现,平移直线可得当直线过点
之间的斜率,结合图象不难发现,平移直线可得当直线过点 处取最大值
处取最大值 ,过点
,过点 处取最小值
处取最小值 .
.
试题解析:(1)设公司每天派出 型卡车
型卡车 辆,
辆,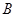 型卡车
型卡车 辆,公司所花的成本费为
辆,公司所花的成本费为 千元,根据题意,得
千元,根据题意,得 ,目标函数
,目标函数 ,作出该不等式组表示的可行域,如下图.
,作出该不等式组表示的可行域,如下图.
考虑 ,变形为
,变形为 ,这是以
,这是以 为斜率,
为斜率, 为
为 轴上的截距的平行直线族.
轴上的截距的平行直线族.
经过可行域,平行移动直线,当直线经过点 时,直线在
时,直线在 轴上的截距最小,即
轴上的截距最小,即 取最小值,为
取最小值,为
答:公司每天派出 型卡车0辆,
型卡车0辆,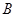 型卡车
型卡车 辆时,所花的成本费最低,为
辆时,所花的成本费最低,为 千元.
千元.
(2)在 处取最大值
处取最大值 ,在
,在 处取最小值
处取最小值 .
.
考点:1.简单的线性规划;2.直线方程;3.两点的斜率坐标公式


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:解答题
某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为保增长、促发展,某地计划投资甲、乙两个项目,根据市场调研,知甲项目每投资100万元需要配套电能2万千瓦时,可提供就业岗位24个,GDP增长260万元;乙项目每投资100万元需要配套电能4万千瓦时,可提供就业岗位36个,GDP增长200万元.已知该地为甲、乙两个项目最多可投资3000万元,配套电能100万千瓦时,若要求两个项目能提供的就业岗位不少于840个,问如何安排甲、乙两个项目的投资额,才能使GDP增长的最多.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司计划2013年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大。已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
| 资 金 | 每台单位产品所需资金(百元) | 月资金供应量 (百元) | |
| 空调机 | 洗衣机 | ||
| 成 本 | 30 | 20 | 300 |
| 劳动力(工资) | 5 | 10 | 110 |
| 每台产品利润 | 6 | 8 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,其中,角
,其中,角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点 ,且
,且 .
.
(1)若 点的坐标为(-
点的坐标为(- ),求
),求 的值;
的值;
(2)若点 为平面区域
为平面区域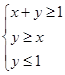 上的一个动点,试确定角
上的一个动点,试确定角 的取值范围,并求函数
的取值范围,并求函数 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
若1<x<10,下面不等式中正确的是 ( )
| A.(lgx)2<lgx2<lg(lgx) |
| B.lgx2<(lgx)2<lg(lgx) |
| C.(lgx)2<lg(lgx)<lgx2 |
| D.lg(lgx)<(lgx)2<lgx2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com