
| 已知:y=f(x)定义域为[-1,1],且满足:f(-1)=f(1)=0,对任意u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|, (1)判断函数p(x)=x2-1是否满足题设条件? (2)判断函数g(x)=  ,是否满足题设条件? ,是否满足题设条件? |
| 解:(1)若u,v∈[-1,1],|p(u)-p(v)|=|u2-v2|=|(u+v)(u-v)|, 取u= 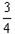 ∈[-1,1],v= ∈[-1,1],v=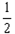 ∈[-1,1], ∈[-1,1],则|p(u)-p(v)|=|(u+v)(u-v)|=  |u-v|>|u-v|, |u-v|>|u-v|,所以p(x)不满足题设条件。 (2)分三种情况讨论: 10.若u,v∈[-1,0],则|g(u)-g(v)|=|(1+u)-(1+v)|=|u-v|,满足题设条件; 20.若u,v∈[0,1],则|g(u)-g(v)|=|(1-u)-(1-v)|=|v-u|,满足题设条件; 30.若u∈[-1,0],v∈[0,1], 则:|g(u)-g(v)|=|(1-u)-(1+v)|=|-u-v|=|v+u|≤|v-u|=|u-v|,满足题设条件; 40.若u∈[0,1],v∈[-1,0],同理可证满足题设条件; 综合上述得g(x)满足条件。 |


科目:高中数学 来源: 题型:
 已知幂函数y=f(x)的图象经过点(2,4),对于偶函数y=g(x)(x∈R),当x≥0时,g(x)=f(x)-2x.
已知幂函数y=f(x)的图象经过点(2,4),对于偶函数y=g(x)(x∈R),当x≥0时,g(x)=f(x)-2x.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.查看答案和解析>>
科目:高中数学 来源: 题型:
| a•2x | ||
2x+
|
| 2 |
| OP |
| 1 |
| 2 |
| OP1 |
| OP2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com