
���� ��1����бʽ���ֱ��l�ķ��̲��������߷������������飬�õ�ֱ��l�����߽���A��B����������Ĺ�ϵ����$\overrightarrow{OP}=\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}$���õ���P��������ֱ��б��k�Ĺ�ϵ����ȥk�õ�����P�Ĺ켣���̣�
��2�����������C������б�ʦ˵ķ�Χ����$\overrightarrow{MB}=��\overrightarrow{MA}$���æ˱�ʾa����б�ʦ˵ķ�Χ�ó�a��ȡֵ��Χ��
��� �⣺��1����ֱ��l�ķ���Ϊy=k��x-1��������ΪA��x1��y1����B��x2��y2����
��$\left\{\begin{array}{l}{x^2}=2y\\ y=k��x-1��\end{array}\right.$����x2-2kx+2k=0������1�֣�
��Ϊֱ�������������������㣬���ԡ�=4k2-8k��0����k��2��k��0..����2�֣�
��$\left\{\begin{array}{l}{x_1}+{x_2}=2k\\{x_1}{x_2}=2k\end{array}\right.$������3�֣�
��$\overrightarrow{OP}=\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}$����P��AB���е㣬��P��x��y����
��$\left\{\begin{array}{l}x=\frac{{{x_1}+{x_2}}}{2}=k\\ y=k��x-1��={k^2}-k\end{array}\right.$����ȥk��y=x2-x������4�֣�
��P����y����Ҳ࣬��x��0������x=k����k��2��k��0����x��2������5�֣�
�ʶ���P�Ĺ켣����Ϊy=x2-x��x��2��������6�֣�
��2��������C�ķ���Ϊy=x2-x��x��2��������C�����ߵ�б��Ϊ��=y'=2x-1��x��2������ˣ�3������7�֣�
����֪�ã�$\left\{\begin{array}{l}\overrightarrow{MB}=��{x_2}-1��{y_2}��\\ \overrightarrow{MA}=��{x_1}-1��{y_1}��\end{array}\right.$
��$\overrightarrow{MB}=��\overrightarrow{MA}$��$\left\{\begin{array}{l}{x_2}-1=�ˣ�{x_1}-1��\\{y_2}=��{y_1}\end{array}\right.$����${x_1}^2=2{y_1}$��${x_2}^2=2{y_2}$��$\left\{\begin{array}{l}{x_2}=��{x_1}-��+1\\{x_2}^2=��{x_1}^2\end{array}\right.$
�֦ˣ�3���$��{x_1}^2-2��{x_1}+��-1=0$������9�֣�
���${x_1}=\frac{{2�ˡ�\sqrt{4��}}}{2��}=1��\sqrt{\frac{1}{��}}$��
��A��y��ľ���Ϊ$a={x_1}=1��\sqrt{\frac{1}{��}}���ˣ�3��$��
��a��ȡֵ��Χ��$��1-\frac{{\sqrt{3}}}{3}��1���ȣ�1��1+\frac{{\sqrt{3}}}{3}��$������12�֣�
���� ���⿼�������߷��̡��켣���̵����Լ��������㣬����ѧ�������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
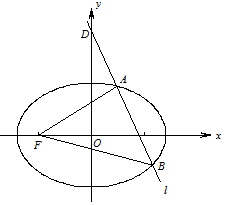 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$������˵�����Բ���������������ɵ����������Ϊ1������D��0��2����б��Ϊk��ֱ��l����Բ��A��B���㣮
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{2}}{2}$������˵�����Բ���������������ɵ����������Ϊ1������D��0��2����б��Ϊk��ֱ��l����Բ��A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
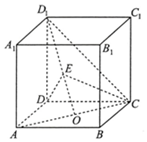 �����ƣ���ͼ����������ABCD-A1B1C1D1��O��AC���е㣬E���߶�D1O��һ�㣬��$\frac{{D}_{1}E}{EO}$=�ˣ�
�����ƣ���ͼ����������ABCD-A1B1C1D1��O��AC���е㣬E���߶�D1O��һ�㣬��$\frac{{D}_{1}E}{EO}$=�ˣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com