
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5 杯,其颜色完全相同,并且其中3杯为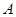 饮料,另外2杯为
饮料,另外2杯为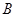 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯
饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯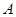 饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对
饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对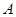 和
和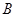 两种饮料没有鉴别能力.
两种饮料没有鉴别能力.
(Ⅰ)求此人被评为优秀的概率;
(Ⅱ)求此人被评为良好及以上的概率.
(Ⅰ)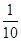 ;(Ⅱ)
;(Ⅱ)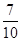 .
.
【解析】
试题分析:根据古典概型的两个特点(基本事件的有限性和每个基本事件发生的等可能性)判断本题属于古典概型,古典概型中,求事件发生的概率,先要求出基本事件数,再求出所求概率事件包含的基本事件数,相比即可.
试题解析:从5杯饮料中任选3杯,所有的选法有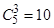 (种)
(种)
(Ⅰ)设“此人被评为优秀”为事件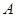 ,即“选中3杯
,即“选中3杯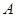 饮料”这个事件发生了,这个事件包含的基本事件数为
饮料”这个事件发生了,这个事件包含的基本事件数为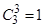 (种),所以事件
(种),所以事件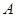 发生的概率为
发生的概率为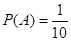 .
.
(Ⅱ)设“此人被评为良好及以上”为事件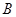 ,即“选中3杯
,即“选中3杯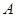 饮料或选中2杯
饮料或选中2杯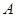 饮料”这个事件发生了,这个事件包含的基本事件数为
饮料”这个事件发生了,这个事件包含的基本事件数为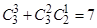 (种),所以事件
(种),所以事件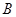 发生的概率为
发生的概率为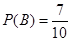 .
.
考点:组合数的计算、古典概型.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:江西 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5
杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工
一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3
杯选对2杯,则评为良好;否则评为及格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
某饮料公司对一名员工进行测试以便确定其考评级别,公司准备了
两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为
B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工
3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为合格.假设
此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com