
【题目】已知函数![]() ,
,![]() (其中
(其中![]() 是自然对数的底数),
是自然对数的底数),
(1)求函数![]() 的单调区间;
的单调区间;
(2)记![]()
①当![]() 时,试判断
时,试判断![]() 的导函数
的导函数![]() 的零点个数;
的零点个数;
②求证:![]() 时,
时,![]()
【答案】(1) ![]() 的单调减区间为
的单调减区间为![]() ,
,![]() 的单调增区间为
的单调增区间为![]() .
.
(2)①存在唯一零点,②证明见解析.
【解析】
(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)①
的减区间;(2)①![]() ,当
,当![]() 时,
时, ![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,可证明存在
,可证明存在![]() 满足
满足![]() 且
且![]() 时,
时,![]() ,从而可得结论;②由①知,可设
,从而可得结论;②由①知,可设![]() 在
在![]() 上存在唯一零点为
上存在唯一零点为![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
将![]() ,
,![]() 代入上式,利用基本不等式可得结论.
代入上式,利用基本不等式可得结论.
(1)![]() ,其定义域为
,其定义域为![]() ,
,
由![]() ,令
,令![]() 得
得![]() ,
,
令![]() 得
得![]() ,
,
∴![]() 的单调减区间为
的单调减区间为![]() ,
,![]() 的单调增区间为
的单调增区间为![]()
(2)①解:由![]()
∴![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递增.
上单调递增.
∴![]() 在
在![]() 上单调递增.
上单调递增.
又![]()
假设存在![]() 满足
满足![]() 且
且![]() 时,
时,![]()
∴当![]() 时
时![]() 在
在![]() 上存在唯一零点.
上存在唯一零点.
②由①知,可设![]() 在
在![]() 上存在唯一零点为
上存在唯一零点为![]() ,
,
∴![]() ,即
,即![]()
两边取自然对数得,![]() ,
,
又当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数;
上是减函数;
![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() ,
,
将![]() ,
,![]() 代入上式得,
代入上式得,
![]()
当且仅当![]() 时等号成立.所以当
时等号成立.所以当![]() 时,
时,![]()


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 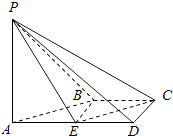
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加
平均增加![]() 个单位;②线性回归直线
个单位;②线性回归直线![]() 必过必过点
必过必过点![]() ;③在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有
;③在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有![]() 的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有
的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有![]() 的可能患肺病;其中错误的个数是( )
的可能患肺病;其中错误的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该批产品还需投入成本
为正常数).已知生产该批产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件
元/件
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;(注:利润=销售收入-促销费-投入成本)
万元的函数;(注:利润=销售收入-促销费-投入成本)
(2)当促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求最后取出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设![]() 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣lnx,a∈R.
(1)求函数f(x)的单调区间;
(2)当x∈(0,e]时,求g(x)=e2x﹣lnx的最小值;
(3)当x∈(0,e]时,证明:e2x﹣lnx﹣ ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) | [0.6,0.7) |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
⑴在答题卡上作出使用了节水龙头
⑵估计该家庭使用节水龙头后,日用水量小于0.35m3的概率;
⑶估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com